题目内容
函数f(x)=xln|x|的大致图象是( )
A、 |
B、 |
C、 |
D、 |
考点:函数的图象
专题:综合题,函数的性质及应用
分析:由于f(-x)=-f(x),得出f(x)是奇函数,其图象关于原点对称,由图象排除C,D,利用导数研究根据函数的单调性质,又可排除选项B,从而得出正确选项.
解答:
解:∵函数f(x)=xln|x|,可得f(-x)=-f(x),
f(x)是奇函数,其图象关于原点对称,排除C,D,
又f′(x)=lnx+1,令f′(x)>0得:x>
,得出函数f(x)在(
,+∞)上是增函数,排除B,
故选A
f(x)是奇函数,其图象关于原点对称,排除C,D,
又f′(x)=lnx+1,令f′(x)>0得:x>
| 1 |
| e |
| 1 |
| e |
故选A
点评:本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
点(x,y)的坐标x,y都是有理数时,该点称为有理点,在半径为r,圆心为(a,b)的圆中,若a∈Q,b∈Q,则这个圆上的有理点的数目为( )
| A、最多有一个 |
| B、最多有两个 |
| C、最多有三个 |
| D、可以有无穷多个 |

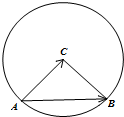 如图,定圆C半径为r,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且
如图,定圆C半径为r,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且