题目内容
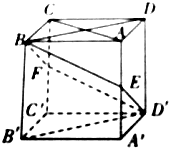 如图,在正方体ABCD-A′B′C′D′中,E,F分别是A′A,C′C的中点,则下列判断中正确的是
如图,在正方体ABCD-A′B′C′D′中,E,F分别是A′A,C′C的中点,则下列判断中正确的是①四边形BFD′E在底面ABCD内的投影是正方形;
②四边形EBFD′在底面A′D′DA内的投影是菱形;
③四边形EBFD′在面A′D′DA内的投影与在面ABB′A′内的投影是全等的平行四边形.
考点:命题的真假判断与应用
专题:阅读型,空间位置关系与距离
分析:运用投影的概念,可得四边形BFD′E在底面ABCD内的投影为B'C'D'A',即可判断①;
四边形BFD′E在底面A′D′DA内的投影为AMD'E,AM>AE,则为平行四边形,即可判断②;
四边形BFD′E在面ABB′A′内的投影是BNA'E,BE>BN,则为平行四边形,即可判断③.
四边形BFD′E在底面A′D′DA内的投影为AMD'E,AM>AE,则为平行四边形,即可判断②;
四边形BFD′E在面ABB′A′内的投影是BNA'E,BE>BN,则为平行四边形,即可判断③.
解答:
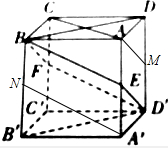 解:对于①,由投影的概念可得四边形BFD′E在底面ABCD内的投影为B'C'D'A',是正方形,则①对;
解:对于①,由投影的概念可得四边形BFD′E在底面ABCD内的投影为B'C'D'A',是正方形,则①对;
对于②,四边形BFD′E在底面A′D′DA内的投影为AMD'E,AM>AE,则为平行四边形,则②错;
对于③,四边形BFD′E在面ABB′A′内的投影是BNA'E,BE>BN,则为平行四边形,且与平行四边形AMD'E全等,则③对.
故答案为:①③.
 解:对于①,由投影的概念可得四边形BFD′E在底面ABCD内的投影为B'C'D'A',是正方形,则①对;
解:对于①,由投影的概念可得四边形BFD′E在底面ABCD内的投影为B'C'D'A',是正方形,则①对;对于②,四边形BFD′E在底面A′D′DA内的投影为AMD'E,AM>AE,则为平行四边形,则②错;
对于③,四边形BFD′E在面ABB′A′内的投影是BNA'E,BE>BN,则为平行四边形,且与平行四边形AMD'E全等,则③对.
故答案为:①③.
点评:本题考查正方体中的投影问题,考查空间想象能力,属于基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
要得到函数y=cos(2x+
)的图象,只需将函数y=cos2x的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
tan(-210°)=( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
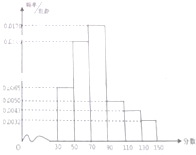 某县为“中学生知识竞赛”进行选取性测试,规定:成绩大于或等于90分的右参赛资格,90分以下(不包括90分)的则被淘汰,若现有1000人参加测试,学生成绩的频率分别直方图如图:
某县为“中学生知识竞赛”进行选取性测试,规定:成绩大于或等于90分的右参赛资格,90分以下(不包括90分)的则被淘汰,若现有1000人参加测试,学生成绩的频率分别直方图如图: