题目内容
抛物线y2=4x的焦点为F(1,0),则以焦点为圆心,且与y轴相切的圆的方程为 .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:得出圆心为F(1,0),半径为F(1,0)与y轴的距离为1,写出圆的方程即可.
解答:
解:∵抛物线y2=4x的焦点为F(1,0),
∴F(1,0)与y轴的距离为1,
∴以焦点为圆心,且与y轴相切的圆的方程为(x-1)2+y2=1,
故答案为:(x-1)2+y2=1.
∴F(1,0)与y轴的距离为1,
∴以焦点为圆心,且与y轴相切的圆的方程为(x-1)2+y2=1,
故答案为:(x-1)2+y2=1.
点评:本题考查了直线与抛物线的位置关系,圆的方程,属于中档题,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设曲线y=ax3在点(1,a)处的切线与直线6x-y+2=0平行,则a=( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
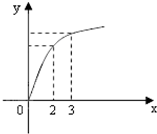 已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )| A、f′(2)<f′(3)<f(3)-f(2) |
| B、f′(3)<f(3)-f(2)<f′(2) |
| C、f′(3)<f′(2)<f(3)-f(2) |
| D、f(3)-f(2)<f′(2)<f′(3) |
已知等差数列{an}共有10项,并且其偶数项之和为30,奇数项之和为25,由此得到的结论正确的是( )
| A、d=1 | ||
B、d=
| ||
| C、a6=5 | ||
| D、a6=-5 |
已知i为虚数单位,图中复平面内的点A表示复数z,则表示复数
的点是( )

| z |
| 1+i |

| A、M | B、N | C、P | D、Q |
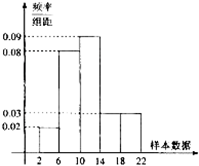 样本容量为200的频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在[6,10)内的
样本容量为200的频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在[6,10)内的