题目内容
9.下面命题判断正确的是( )| A. | 若p∨q是真命题,则p,q都是真命题 | |
| B. | 命题“?x0∈R,x02-1>0的否定是“?x∈R,x2-1<0” | |
| C. | 过平面α外的一点P的直线与平面α所成的角为θ,则这样的直线有无数条 | |
| D. | △ABC中,“A>B”是“sinA>sinB”的充要条件 |
分析 A,若p∨q是真命题,则p,q至少有一个是真命题;
B,命题“?x0∈R,x02-1>0的否定是“?x∈R,x2-1≤0”.
C,过平面α外的一点P的直线与平面α所成的角为θ,当θ=900时,这样的直线有一数条;
D,由正弦定理知 asinA=bsinB,由sinA>sinB,知a>b,所以A>B,反之亦然.
解答 解:对于A,若p∨q是真命题,则p,q至少有一个是真命题,故错;
对于B,命题“?x0∈R,x02-1>0的否定是“?x∈R,x2-1≤0”,故错.
对于C,过平面α外的一点P的直线与平面α所成的角为θ,当θ=900时,这样的直线有一数条故错;
对于D,由正弦定理知 asinA=bsinB,由sinA>sinB,知a>b,所以A>B,反之亦然,故正确.
故选:D
点评 本题考查了命题真假的判定,涉及到了复合命题、特称命题、充要条件的知识,属于中档题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
4.如图所示,在△ABC中,D为BC的中点,BP丄DA,垂足为P,且BP=2,则$\overrightarrow{BC}$•$\overrightarrow{BP}$=( )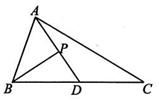

| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
19.对实数a与b,定义新运算“?”:a?b=$\left\{\begin{array}{l}{a,a-b≤1}\\{b,a-b>1}\end{array}\right.$.设函数f(x)=(x2-2)?(x-x2),x∈R.若函数y=f(x)-c的零点恰有两个,则实数c的取值范围是( )
| A. | (-∞,-2]∪(-1,$\frac{3}{2}$) | B. | (-∞,-2]∪(-1,-$\frac{3}{4}$) | C. | (-∞,$\frac{1}{4}$)∪($\frac{1}{4}$,+∞) | D. | (-1,-$\frac{3}{4}$)∪[$\frac{1}{4}$,+∞) |
 如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,若M为线段A1C的中点,则在△ADE翻转过程中,对于下列说法:
如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,若M为线段A1C的中点,则在△ADE翻转过程中,对于下列说法: