题目内容
1-90C
+902C
-903C
+…+(-1)k90kC
+…+9010C
除以88的余数是 .
1 10 |
2 10 |
3 10 |
k 10 |
10 10 |
考点:二项式系数的性质
专题:二项式定理
分析:把所给的式子化为 (1+88)10,再利用二项式定理展开可得它除以88的余数.
解答:
解:∵1-90C
+902C
-903C
+…+(-1)k90kC
+…+9010C
=(1-90)10
=(1+88)10=
+
×88+
×882+…+
×8810,
故它除以88的余数为
=1,
故答案为:1.
1 10 |
2 10 |
3 10 |
k 10 |
10 10 |
=(1+88)10=
| C | 0 10 |
| C | 1 10 |
| C | 2 10 |
| C | 10 10 |
故它除以88的余数为
| C | 0 10 |
故答案为:1.
点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,把所给的式子化为 (1+88)10,是解题的关键,属于基础题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
在△ABC中,a=3,b=6,sinC=
,则△ABC的面积为( )
| ||
| 3 |
A、
| ||
B、2
| ||
C、4
| ||
D、3
|
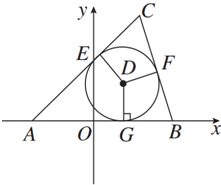 △ABC的顶点A(-5,0),B(5,0),△ABC的内切圆圆心在直线x=3上,则顶点C的轨迹方程是
△ABC的顶点A(-5,0),B(5,0),△ABC的内切圆圆心在直线x=3上,则顶点C的轨迹方程是