题目内容
函数f(x)＝(x－2)(ax＋b)为偶函数，且在(0，＋∞)单调递增，则f(2－x)＞0的解集为( )
A．{x|x＞2或x＜－2}
B．{x|－2＜x＜2}
C．{x|x＜0或x＞4}
D．{x|0＜x＜4}
C
[解析] ∵f(x)＝ax2＋(b－2a)x－2b为偶函数，∴b－2a＝0，即b＝2a，∴f(x)＝ax2－4a.∴f′(x)＝2ax.又∵f(x)在(0，＋∞)单调递增，∴a＞0.由f(2－x)＞0，得a(x－2)2－4a＞0，∵a＞0，∴|x－2|＞2，解得x＞4或x＜0.
练习册系列答案
相关题目
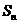是数列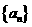
的前n项和，且
．
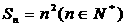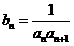，求数列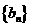
的前n项和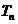
．
≤0的解集为( )
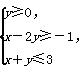表示的平面区域内的任意一点，向量m＝(1,1)，n＝(2,1)，若
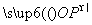＝λm＋μn(λ，μ∈R)，则μ的最大值为( )
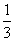C．0 D．－1
若存在k使得函数f(x)的值域是[0,2]，则实数a的取值范围是( )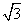
，＋∞) B.