题目内容
抛物线y2=2x上有一点P，P点的横坐标x=2，则P到抛物线的焦点的距离为 ．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：直接利用抛物线的定义，求解即可．
解答：
解：抛物线y2=2x上横坐标为2的点到其焦点的距离，
就是这点到抛物线的准线的距离．
抛物线的准线方程为：x=-
，
所以抛物线y2=2x上横坐标为2的点到其焦点的距离为
+2=
．
故答案为：
．
就是这点到抛物线的准线的距离．
抛物线的准线方程为：x=-
| 1 |
| 2 |
所以抛物线y2=2x上横坐标为2的点到其焦点的距离为
| 1 |
| 2 |
| 5 |
| 2 |
故答案为：
| 5 |
| 2 |
点评：本题考查抛物线的简单性质的应用，抛物线的定义的应用，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
根据如下样本数据：
得到的回归方程为
=
x+
，则（ ）
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 2.5 | -0.5 | 0.5 | -2 | -3 |
| ? |
| y |
| ? |
| b |
| ? |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=3x-8+log2x的零点一定位于的区间为（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
若{2，3}?M?{1，2，3，4，5}，则M的个数为（ ）
| A、5 | B、6 | C、7 | D、8 |
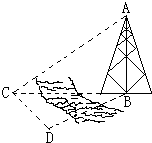如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C与D，测得∠BCD=75°，∠BDC=60°，CD=40（米），并在点C测得塔顶A的仰角为30°．则塔高AB=