题目内容
16.在平面直角坐标系中,动点P到点F(1,0)的距离比它到y轴的距离多1,记点P的轨迹为曲线C,给出下列三个结论:①曲线C过坐标原点;
②曲线C关于x轴对称;
③曲线C的轨迹是抛物线.
其中,所有正确结论的序号是①②.
分析 设动点M的坐标为(x,y),根据动点M到点F(1,0)的距离比它到y轴的距离大1,建立方程,化简可得点M的轨迹C的方程,即可判断结论.
解答 解:设动点M的坐标为(x,y),
由题意,∵动点M到点F(1,0)的距离比它到y轴的距离大1,
∴$\sqrt{(x-1)^{2}+{y}^{2}}$=|x|+1;
化简得y2=4x(x≥0)或y=0(x≤0),
∴①曲线C过坐标原点,正确;
②曲线C关于x轴对称,正确;
③曲线C的轨迹是抛物线,不正确.
故答案为:①②.
点评 本题考查轨迹方程,考查了直线与圆锥曲线的关系,考查了学生数形结合的思想和分析推理能力,是中档题.

练习册系列答案
相关题目
11.假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下的统计资料:
由资料可知y对x呈线性相关关系,且线性回归方程为$\hat y=1.2x+a$,请估计使用年限为20年时,维修费用约为( )
| x | 1 | 2 | 3 | 4 | 5 |
| y | 5 | 6 | 7 | 8 | 10 |
| A. | 26.2 | B. | 27 | C. | 27.6 | D. | 28.2 |
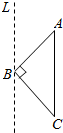 如图,等腰直角三角形ABC,|AB|=$\sqrt{2}$,AC∥L,三角形ABC绕直线L旋转一周,得到的几何体的体积为$\frac{4π}{3}$.
如图,等腰直角三角形ABC,|AB|=$\sqrt{2}$,AC∥L,三角形ABC绕直线L旋转一周,得到的几何体的体积为$\frac{4π}{3}$.