题目内容
设P的极坐标为（2，
），直线l过点P，且与θ=
平行，则直线l的极坐标方程为 ．
| π |
| 6 |
| π |
| 4 |
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：利用
即可实现极坐标与直角坐标方程的互化．
|
解答：
解：由P的极坐标为（2，
），可得xP=2cos
=
，yP=2sin
=1，∴P(
，1)．
直线θ=
即为直线y=x．
直线l与直线y=x平行，因此l的斜率为1．
∴直线l的方程为：y-1=x-
，
化为极坐标方程ρcosθ-ρsinθ+1-
=0，
故答案为：ρcosθ-ρsinθ+1-
=0，
| π |
| 6 |
| π |
| 6 |
| 3 |
| π |
| 6 |
| 3 |
直线θ=
| π |
| 4 |
直线l与直线y=x平行，因此l的斜率为1．
∴直线l的方程为：y-1=x-
| 3 |
化为极坐标方程ρcosθ-ρsinθ+1-
| 3 |
故答案为：ρcosθ-ρsinθ+1-
| 3 |
点评：本题考查了极坐标与直角坐标方程的互化，属于基础题．
练习册系列答案
相关题目
已知ABCD是正方形，PA⊥面ABCD，且PA=AB，E，F是侧棱PD，PC的中点．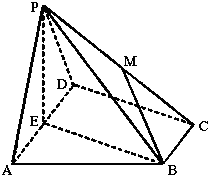
如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，E为AD的中点，M是棱PC的中点，PA=PD=2，BC=