题目内容
已知函数f(x)=
(ax-a-x),(a>0,a≠1)
(1)判断并证明f(x)的单调性;
(2)若当x∈(-∞,2)时,f(x)-4<0恒成立,求a得取值范围.
| a |
| a2-1 |
(1)判断并证明f(x)的单调性;
(2)若当x∈(-∞,2)时,f(x)-4<0恒成立,求a得取值范围.
考点:函数单调性的判断与证明,函数恒成立问题
专题:函数的性质及应用
分析:(1)分a>1和 0<a<1两种情况,利用函数的单调性的定义,证明f(x)在R上的单调性.
(2)因为f(x)在(-∞,2)单调递增,f(x)-4<0恒成立,可得
(a2-a-2)≤4,由此解得a的范围.
(2)因为f(x)在(-∞,2)单调递增,f(x)-4<0恒成立,可得
| a |
| a2-1 |
解答:
解:(1)f(x)在R上是增函数.
证明:任取x1,x2∈R,且x1<x2 ,
由于f(x1)-f(x2)=
(ax1-a-x2)-
(ax2-a-x2)
=
(ax1-ax2)•
,
由题设可得 ax1ax2+1>0,ax1ax2>0,
当a>1时,因为x1<x2,ax1-ax2<0,
>0,
所以f(x1)-f(x2)<0,即f(x1)<f(x2),∴f(x)在R上是增函数.
当0<a<1时,因为x1<x2,ax1-ax2>0,
<0,
所以f(x1)-f(x2)<0,即f(x1)<f(x2),∴f(x)在R上是增函数.
综上,f(x)在R上是增函数.
(2)因为f(x)在(-∞,2)单调递增,f(x)-4<0恒成立,
所以
(a2-a-2)≤4,解得 2-
≤a≤2+
且a≠1,
故a的范围为[2-
,1)∪(1,2+
].
证明:任取x1,x2∈R,且x1<x2 ,
由于f(x1)-f(x2)=
| a |
| a2-1 |
| a |
| a2-1 |
=
| a |
| a2-1 |
| ax1ax2+1 |
| ax1ax2 |
由题设可得 ax1ax2+1>0,ax1ax2>0,
当a>1时,因为x1<x2,ax1-ax2<0,
| a |
| a2-1 |
所以f(x1)-f(x2)<0,即f(x1)<f(x2),∴f(x)在R上是增函数.
当0<a<1时,因为x1<x2,ax1-ax2>0,
| a |
| a2-1 |
所以f(x1)-f(x2)<0,即f(x1)<f(x2),∴f(x)在R上是增函数.
综上,f(x)在R上是增函数.
(2)因为f(x)在(-∞,2)单调递增,f(x)-4<0恒成立,
所以
| a |
| a2-1 |
| 3 |
| 3 |
故a的范围为[2-
| 3 |
| 3 |
点评:本题主要考查函数的单调性的判断和证明,函数的恒成立问题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
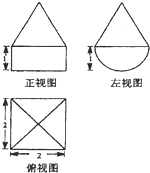 某几何体的三视图如图所示,其中正视图和左视图的上半部分均为边长为2的等边三角形,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图和左视图的上半部分均为边长为2的等边三角形,则该几何体的体积为( )A、π+
| ||||
B、2π+
| ||||
C、π+
| ||||
D、2π+
|
不等式x-2y+5>0表示的区域在直线x-2y+5=0的( )
| A、右上方 | B、右下方 |
| C、左上方 | D、左下方 |
 某制造商3月生产了一批乒乓球,随机抽取100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表:
某制造商3月生产了一批乒乓球,随机抽取100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表: