题目内容
已知椭圆G:
+y2=1,过点(m,0)作圆x2+y2=1的切线L交椭圆G于A,B两点.
(1)求椭圆G的焦点坐标和离心率;
(2)求m的取值范围;
(3)将|AB|表示为m的函数,并求|AB|的最大值.
| x2 |
| 4 |
(1)求椭圆G的焦点坐标和离心率;
(2)求m的取值范围;
(3)将|AB|表示为m的函数,并求|AB|的最大值.
考点:圆与圆锥曲线的综合,两点间的距离公式,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)由椭圆G:
+y2=1,可得a2=4,b2=1,利用c=
即可得出椭圆的焦点坐标为(±
,0),e=
..
(2)由题意可知:|m|≥1.当m≠±1时,设切线L的方程为:y=k(x-m).利用直线L与圆x2+y2=1相切可得圆心(0,0)到直线的距离d=r,可得k2m2=1+k2.(*)直线L的方程与椭圆的方程联立,化为(1+4k2)x2-8k2mx+4k2m2-4=0,由于直线L与椭圆由两个不同的交点,可得△>0,即可得到m的取值范围.
(3)当m±1时,直接得出|AB|.当m≠±1时,由(1)可得x1+x2=
,x1x2=
.利用弦长公式|AB|=
,再利用基本不等式即可得出.
| x2 |
| 4 |
| a2-b2 |
| 3 |
| c |
| a |
(2)由题意可知:|m|≥1.当m≠±1时,设切线L的方程为:y=k(x-m).利用直线L与圆x2+y2=1相切可得圆心(0,0)到直线的距离d=r,可得k2m2=1+k2.(*)直线L的方程与椭圆的方程联立,化为(1+4k2)x2-8k2mx+4k2m2-4=0,由于直线L与椭圆由两个不同的交点,可得△>0,即可得到m的取值范围.
(3)当m±1时,直接得出|AB|.当m≠±1时,由(1)可得x1+x2=
| 8k2m |
| 1+4k2 |
| 4k2m2-4 |
| 1+4k2 |
| (1+k2)[(x1+x2)2-4x1x2] |
解答:
解:(1)由椭圆G:
+y2=1,可得a2=4,b2=1,∴c=
=
,∴椭圆的焦点坐标为(±
,0),e=
=
.
(2)由题意可知:|m|≥1.
当m≠±1时,设切线L的方程为:y=k(x-m).
∵直线L与圆x2+y2=1相切,∴圆心(0,0)到直线的距离d=r,∴
=1,化为k2m2=1+k2.(*)
直线L的方程与椭圆的方程联立
,化为(1+4k2)x2-8k2mx+4k2m2-4=0,
∵直线L与椭圆由两个不同的交点,∴△>0,即64k4m2-16(1+4k2)(k2m2-1)>0,
化为1+4k2>k2m2,
把(*)代入上式可得1+
>
,化为m2-1>0.解得m>1或m<-1.
当m=±1时,直接验证满足题意.
综上可知:m的取值范围为(-∞,-1]∪[1,+∞).
(3)当m=1时,切线L的方程为x=1,联立
,解得
,|AB|=
.
同理m=-1时,|AB|=
.
当m≠±1时,由(2)可得x1+x2=
,x1x2=
.
∴|AB|=
=
=
=
≤2.由基本不等式可知当且仅当m=±
时取等号.
综上可知:|AB|的最大值为2.
| x2 |
| 4 |
| a2-b2 |
| 3 |
| 3 |
| c |
| a |
| ||
| 2 |
(2)由题意可知:|m|≥1.
当m≠±1时,设切线L的方程为:y=k(x-m).
∵直线L与圆x2+y2=1相切,∴圆心(0,0)到直线的距离d=r,∴
| |km| | ||
|
直线L的方程与椭圆的方程联立
|
∵直线L与椭圆由两个不同的交点,∴△>0,即64k4m2-16(1+4k2)(k2m2-1)>0,
化为1+4k2>k2m2,
把(*)代入上式可得1+
| 4 |
| m2-1 |
| m2 |
| m2-1 |
当m=±1时,直接验证满足题意.
综上可知:m的取值范围为(-∞,-1]∪[1,+∞).
(3)当m=1时,切线L的方程为x=1,联立
|
|
| 3 |
同理m=-1时,|AB|=
| 3 |
当m≠±1时,由(2)可得x1+x2=
| 8k2m |
| 1+4k2 |
| 4k2m2-4 |
| 1+4k2 |
∴|AB|=
| (1+k2)[(x1+x2)2-4x1x2] |
(1+k2)[
|
4
| ||
| m2+3 |
4
| ||
|m|+
|
| 3 |
综上可知:|AB|的最大值为2.
点评:本题综合考查了直线与圆相切、直线与椭圆相交问题转化为方程联立得到△>0及根与系数的关系、弦长公式、基本不等式等基础知识与基本技能方法,考查了推理能力、计算能力,属于难题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
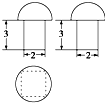 已知一个几何体的三视图如图所示,则该几何体的表面积为( )
已知一个几何体的三视图如图所示,则该几何体的表面积为( )| A、24+6π |
| B、24+4π |
| C、28+6π |
| D、28+4π |
 某制造商3月生产了一批乒乓球,随机抽取100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表:
某制造商3月生产了一批乒乓球,随机抽取100个进行检查,测得每个球的直径(单位:mm),将数据分组如下表: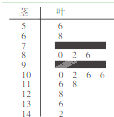 某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取20名学生的成绩进行分析,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下: