题目内容
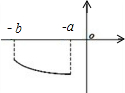
已知f（x）在定义域上是奇函数，且在[a，b]（0＜a＜b）上是减函数，图象如图所示．（1）化简：f（
| 2a+b |
| 3 |
| a+2b |
| 3 |
| -2a-b |
| 3 |
| -a-2b |
| 3 |
（2）画出函数f（x）在[-b，-a]上的图象；
（3）证明：f（x）在[-b，-a]上是减函数．
考点：奇偶函数图象的对称性
专题：函数的性质及应用
分析：（1）根据函数是奇函数，可将原式化为f（
）+f（
）-f（
）+f（
），进而得到答案．
（2）根据奇函数的图象关于原点对称，可由函数在[a，b]（0＜a＜b）上的图象，对称变换后画出函数f（x）在[-b，-a]上的图象；
（3）任取x1，x2∈[-b，-a]，且x1＜x2，根据函数的单调性和奇偶性，结合函数在[a，b]（0＜a＜b）上是减函数，可判断出f（x）在[-b，-a]上是减函数．
| 2a+b |
| 3 |
| a+2b |
| 3 |
| 2a+b |
| 3 |
| a+2b |
| 3 |
（2）根据奇函数的图象关于原点对称，可由函数在[a，b]（0＜a＜b）上的图象，对称变换后画出函数f（x）在[-b，-a]上的图象；
（3）任取x1，x2∈[-b，-a]，且x1＜x2，根据函数的单调性和奇偶性，结合函数在[a，b]（0＜a＜b）上是减函数，可判断出f（x）在[-b，-a]上是减函数．
解答：
解：（1）∵f（x）在定义域上是奇函数，
∴f（
）+f（
）+f（
）+f（
）
=f（
）+f（
）-f（
）+f（
）
=0
（2）根据f（x）在定义域上是奇函数，可得函数的图象关于原点对称
故函数f（x）在[-b，-a]上的图象
如下图所示
证明：（3）任取x1，x2∈[-b，-a]，且x1＜x2，
∵-b≤x1＜x2≤-a
∴a≤-x2＜-x1≤b
又∵f（x）在[a，b]上是减函数，
∴f（-x2）＞f（-x1）
∵f（x）在定义域上是奇函数，
∴-f（x2）＞-f（x1）
即f（x2）＜f（x1）
故f（x）在[-b，-a]上是减函数
∴f（
| 2a+b |
| 3 |
| a+2b |
| 3 |
| -2a-b |
| 3 |
| -a-2b |
| 3 |
=f（
| 2a+b |
| 3 |
| a+2b |
| 3 |
| 2a+b |
| 3 |
| a+2b |
| 3 |
=0
（2）根据f（x）在定义域上是奇函数，可得函数的图象关于原点对称
故函数f（x）在[-b，-a]上的图象
如下图所示
证明：（3）任取x1，x2∈[-b，-a]，且x1＜x2，
∵-b≤x1＜x2≤-a
∴a≤-x2＜-x1≤b
又∵f（x）在[a，b]上是减函数，
∴f（-x2）＞f（-x1）
∵f（x）在定义域上是奇函数，
∴-f（x2）＞-f（x1）
即f（x2）＜f（x1）
故f（x）在[-b，-a]上是减函数
点评：本题考查的知识点是函数的奇偶性，与函数的单调性，是函数图象和性质的简单综合应用，难度不大，属基础题．
练习册系列答案
相关题目
若实数x，y能使式子
-
+lg(1+
)有意义，则z=2x-y的最小值是（ ）
| x-y+1 |
| x+y |
| -x |
| A、1 | ||
| B、0 | ||
| C、-1 | ||
D、-
|
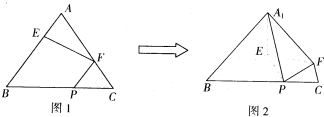如图1，在正三角形ABC中，已知AB=5，E、F、P分别是AB、AC、BC边上的点，设