题目内容
已知a＞b＞0，ab=1，则
的最小值为 ．
| a2+b2 |
| a-b |
考点：基本不等式
专题：不等式的解法及应用
分析：本题是基本不等式问题，可以利用a＞b＞0得到a-b＞0（正数），再利用条件ab为定值将a2+b2转化为（a-b）2与ab，化简后，运用基本不等式解决问题．
解答：
解：∵a＞b＞0，ab=1∴a-b＞0
∴
=
=(a-b)+
≥2
=2
当且仅当a-b=
时取等号
故答案为2
∴
| a2+b2 |
| a-b |
| (a-b)2+2ab |
| a-b |
| 2 |
| a-b |
(a-b)
|
| 2 |
当且仅当a-b=
| 2 |
故答案为2
| 2 |
点评：本题主要考查了基本不等式的应用和转化化归的数学思想，注意不等式成立的条件（一正二定三相等）
练习册系列答案
相关题目
在△ABC中，AB=AC=2，∠B=30°，P为BC边中线上的任意一点，则
•
的值为（ ）
| CP |
| BC |
| A、-12 | B、-6 | C、6 | D、12 |
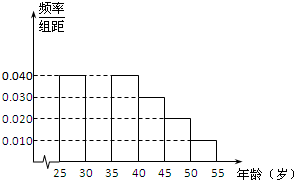某班研究性学习小组在今年11月11日“双11购物节”期间，对[25，55）岁的人群随机抽取了1000人进行了一次是否参加“抢购商品”的调查，得到如下统计表和各年龄段人数频率分布直方图． 
某校高一年级共有320人，为调查高一年级学生每天晚自习自主支配学习时间（指除了完成老师布置的作业后学生根据自己的需要进行学习的时间）情况，学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查．根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据（单位：分钟），按照以下区间分为七组：①[0，10），②[10，20），③[20，30），④[30，40），⑤[40，50），⑥[50，60），⑦[60，70），得到频率分布直方图如图．已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人．