题目内容
已知函数f（x）=sinx+
cosx，x∈[0，
]．
（1）当函数取得最大值时，求自变量x的值；
（2）若方程f（x）-a=0有两个实数根，求a的取值范围．
| 3 |
| π |
| 2 |
（1）当函数取得最大值时，求自变量x的值；
（2）若方程f（x）-a=0有两个实数根，求a的取值范围．
考点：两角和与差的正弦函数,正弦函数的图象
专题：三角函数的求值
分析：（1）化简可得f（x）=2sin（x+
），易得当x=
时，函数取最大值；
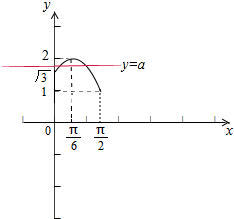
（2）问题等价于f（x）与y=a有两个不同的交点，作图象易得a的取值范围．
| π |
| 3 |
| π |
| 6 |
（2）问题等价于f（x）与y=a有两个不同的交点，作图象易得a的取值范围．
解答：
解：（1）化简可得f（x）=sinx+
cosx
=2（
sinx+
cosx）=2sin（x+
），
∵由已知可得x∈[0，
]，
∴当x+
=
即x=
时，函数取最大值；
（2）方程f（x）-a=0有两个实数根，
等价于f（x）与y=a有两个不同的交点，
作图象可得a的取值范围为：[
，2）
解：（1）化简可得f（x）=sinx+| 3 |
=2（
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∵由已知可得x∈[0，
| π |
| 2 |
∴当x+
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
（2）方程f（x）-a=0有两个实数根，
等价于f（x）与y=a有两个不同的交点，
作图象可得a的取值范围为：[
| 3 |
点评：本题考查两角和与差的三角函数公式，等价转化并作图是解决问题的关键，属中档题．
练习册系列答案
相关题目
已知命题P：?a，b（0，+∞），当a+b=1时，
+
=3； 命题Q：?x∈R，x2-x+1≥0恒成立，则下列命题是假命题的是（ ）
| 1 |
| a |
| 1 |
| b |
| A、￢P∨￢Q | B、￢P∧￢Q |
| C、￢P∨Q | D、￢P∧Q |
在△ABC中，a=8，B=60°，c=4（
+1），则b等于（ ）
| 3 |
A、2
| ||
B、4
| ||
C、4（
| ||
D、4
|
记F（x，y）=（x-y）2+（
+
）2（y≠0），则F（x，y）的最小值是（ ）
| x |
| 3 |
| 3 |
| y |
A、
| ||
B、
| ||
C、
| ||
| D、4 |
函数f（x）=x+x3（x∈R）当0＜θ＜
时，f（asinθ）+f（1-a）＞0恒成立，则实数a的取值范围是（ ）
| π |
| 2 |
| A、（-∞，1] |
| B、（-∞，1） |
| C、（1，+∞） |
| D、（1，+∞） |