题目内容
12.点M的直角坐标($\sqrt{3}$,-1)化成极坐标为( )| A. | (2,$\frac{5π}{6}$) | B. | (2,$\frac{2π}{3}$) | C. | (2,$\frac{5π}{3}$) | D. | (2,$\frac{11π}{6}$) |
分析 根据x=ρcosθ,y=ρsinθ,可得极坐标.
解答 解:点M的直角坐标($\sqrt{3}$,-1)
由x=ρcosθ,y=ρsinθ,
∴$\sqrt{3}$=ρcosθ,-1=ρsinθ,
解得:ρ=2,θ=$\frac{11π}{6}$,
∴极坐标为(2,$\frac{11π}{6}$)
故选D.
点评 本题考查了直角坐标化成极坐标的计算.要牢记x=ρcosθ,y=ρsinθ的关系.比较基础.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
17.“ab<0”是“方程ax2+by2=c表示双曲线”的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不必要也不充分条件 |
7.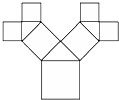 如图所示,正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形…,如此继续,若共得到1023个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为( )
如图所示,正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形…,如此继续,若共得到1023个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为( )
 如图所示,正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形…,如此继续,若共得到1023个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为( )
如图所示,正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形…,如此继续,若共得到1023个正方形,设初始正方形的边长为$\frac{{\sqrt{2}}}{2}$,则最小正方形的边长为( )| A. | $\frac{1}{64}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{32}$ | D. | $\frac{1}{8}$ |
17.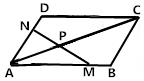 如图,在?ABCD中,M,N分别为AB,AD上的点,且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC,MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
如图,在?ABCD中,M,N分别为AB,AD上的点,且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC,MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
 如图,在?ABCD中,M,N分别为AB,AD上的点,且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC,MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )
如图,在?ABCD中,M,N分别为AB,AD上的点,且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$,连接AC,MN交于P点,若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$,则λ的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{7}$ | C. | $\frac{6}{13}$ | D. | $\frac{6}{17}$ |
2.若a<0,则$\sqrt{a{x^3}}$=( )
| A. | x$\sqrt{ax}$ | B. | x$\sqrt{-ax}$ | C. | -x$\sqrt{-ax}$ | D. | -x$\sqrt{ax}$ |