题目内容
17.“ab<0”是“方程ax2+by2=c表示双曲线”的( )| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不必要也不充分条件 |
分析 运用反例,特殊值,结合双曲线的标准方程判断.
解答 解:若a=1,b=-1,c=0,则不能表示双曲线,不是充分条件,
反之,若方程ax2+by2=c表示双曲线,
则a,b异号,是必要条件,
故ab<0是方程ax2+by2=c表示双曲线的必要不充分条件,
故选:C.
点评 本题考查了充分必要条件的定义,双曲线的标准方程,属于基础题.

练习册系列答案
相关题目
7.过点(2,1)作圆(x-1)2+(y+2)2=25的弦,其中最短的弦所在的直线方程为( )
| A. | 3x-y-5=0 | B. | x+3y-1=0 | C. | 2x-y-3=0 | D. | x+3y-5=0 |
8.“0≤a<2”是“ax2+2ax+1>0的解集是实数集R”的( )
| A. | 充分而非必要条件 | B. | 必要而非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
5.等比数列{an}中,an∈R+,a4•a5=32,则log2a1+log2a2+…+log2a8的值为( )
| A. | 10 | B. | 20 | C. | 36 | D. | 128 |
2.已知函数f(x)=-x3+ax在区间[-2,1]上是单调增函数,则实数a的最小值是( )
| A. | 12 | B. | 0 | C. | 3 | D. | 1 |
12.点M的直角坐标($\sqrt{3}$,-1)化成极坐标为( )
| A. | (2,$\frac{5π}{6}$) | B. | (2,$\frac{2π}{3}$) | C. | (2,$\frac{5π}{3}$) | D. | (2,$\frac{11π}{6}$) |
13.已知函数$f(x)=\left\{\begin{array}{l}{log_2}x,x>0\\{2^x},x≤0\end{array}\right.$,则$f[f(\frac{1}{4})]$=( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | $-\frac{1}{4}$ |
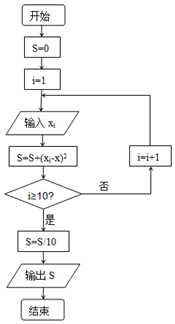 三月植树节,林业管理部门在植树前,为了保证树苗的质量,都会在植树前对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):
三月植树节,林业管理部门在植树前,为了保证树苗的质量,都会在植树前对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):