题目内容
已知函数f(x)为奇函数,且当x>0时,f(x)=x2+
+lnx,则f(-1)=( )
| 1 |
| x |
| A、-2 | B、0 | C、1 | D、2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数奇偶性的性质将条件进行转化即可得到结论.
解答:
解:∵函数f(x)为奇函数,
∴f(-1)=-f(1)=-(1+1+lnx1)=-2,
故选:A
∴f(-1)=-f(1)=-(1+1+lnx1)=-2,
故选:A
点评:本题主要考查函数值的计算,根据函数的奇偶性将条件进行转化是解决本题的关键.

练习册系列答案
相关题目
设全集U={1,2,3,4,5},M={3,4},N={2,3},则图中阴影部分所表示的集合是( )
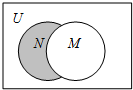

| A、{1,2,4} |
| B、{2,4} |
| C、{2} |
| D、{1,2,5} |
不等式x2-3x+2>0的解集为( )
| A、(-∞,-2)∪(-1,+∞) |
| B、(-∞,1)∪(2,+∞) |
| C、(-2,-1) |
| D、(1,2) |
袋中共有6个除了颜色外完全相同的球,其中有1个红球,2个白球和3个黑球,从袋中任取1球,则取出的球为恰好是黑球的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知an=(
已知an=(| 1 |
| 3 |
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
设随机变量ξ~N(μ,σ2),且P(ξ≤c)=P(ξ>c)=p,则p的值为:( )
| A、0 | B、0.5 | C、1 | D、不确定 |