题目内容
12.设θ∈R,则“|θ-$\frac{π}{12}$|<$\frac{π}{12}$”是“sinθ<$\frac{1}{2}$”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 运用绝对值不等式的解法和正弦函数的图象和性质,化简两已知不等式,结合充分必要条件的定义,即可得到结论.
解答 解:|θ-$\frac{π}{12}$|<$\frac{π}{12}$?-$\frac{π}{12}$<θ-$\frac{π}{12}$<$\frac{π}{12}$?0<θ<$\frac{π}{6}$,
sinθ<$\frac{1}{2}$?-$\frac{7π}{6}$+2kπ<θ<$\frac{π}{6}$+2kπ,k∈Z,
则(0,$\frac{π}{6}$)?[-$\frac{7π}{6}$+2kπ,$\frac{π}{6}$+2kπ],k∈Z,
可得“|θ-$\frac{π}{12}$|<$\frac{π}{12}$”是“sinθ<$\frac{1}{2}$”的充分不必要条件.
故选:A.
点评 本题考查充分必要条件的判断,同时考查正弦函数的图象和性质,运用定义法和正确解不等式是解题的关键,属于基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
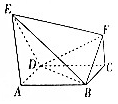 如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.
如图,正方形ABCD的边长为1,E,F是平面ABCD同一侧的两点,AE∥FC,AE⊥AB,AE=1,DE=$\sqrt{2}$,FC=$\frac{1}{2}$.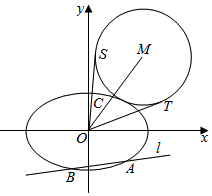 在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,焦距为2.
在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,焦距为2.