题目内容
12.由曲线y=x2,y2=x所围成图形的面积为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
分析 先画出图形,再根据定积分即可求出.
解答  解:联立方程组$\left\{\begin{array}{l}{y={x}^{2}}\\{{y}^{2}=x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
解:联立方程组$\left\{\begin{array}{l}{y={x}^{2}}\\{{y}^{2}=x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,
则曲线y=x2,y2=x所围成图形的面积为
S=2${∫}_{0}^{1}$(x-x2)dx=2($\frac{1}{2}{x}^{2}-\frac{1}{3}{x}^{3}$)|${\;}_{0}^{1}$=$\frac{1}{3}$,
故选:A
点评 本题考查了定积分在面积中的应用,属于基础题.

练习册系列答案
相关题目
7.已知向量$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(4,-2),若$\overrightarrow{a}$$⊥\overrightarrow{b}$,则m=( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
17.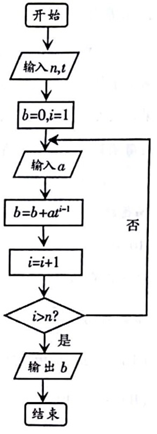 在生活中,我们需要把k进制数化为十进制数,如图是实现该算法的程序框图.执行该程序框图,若输入n=5,t=3,依次输入的a的值为2,0,1,2,1,则输出结果是( )
在生活中,我们需要把k进制数化为十进制数,如图是实现该算法的程序框图.执行该程序框图,若输入n=5,t=3,依次输入的a的值为2,0,1,2,1,则输出结果是( )
 在生活中,我们需要把k进制数化为十进制数,如图是实现该算法的程序框图.执行该程序框图,若输入n=5,t=3,依次输入的a的值为2,0,1,2,1,则输出结果是( )
在生活中,我们需要把k进制数化为十进制数,如图是实现该算法的程序框图.执行该程序框图,若输入n=5,t=3,依次输入的a的值为2,0,1,2,1,则输出结果是( )| A. | 179 | B. | 178 | C. | 147 | D. | 146 |
1.若${(1+i)^2}+|2i|=\bar z$,其中z=a+bi(a,b∈R,i为虚数单位),则直线bx-ay+a=0的斜率为( )
| A. | -2 | B. | -1 | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
 一个几何体的三视图(单位:cm)如图所示,则该几何体的表面积是12+4πcm2.
一个几何体的三视图(单位:cm)如图所示,则该几何体的表面积是12+4πcm2.