题目内容

已知O＜θ＜
π
2
，求tanθ+
1
tanθ
的最小值．
考点：基本不等式
专题：不等式的解法及应用
分析：由于O＜θ＜
π
2
，可得tanθ＞0．再利用基本不等式即可得出．
解答： 解：∵O＜θ＜
π
2
，
∴tanθ＞0．
∴tanθ+
1
tanθ
≥2
tanθ•
1
tanθ
=2，当且仅当tanθ=1即θ=
π
4
时取等号．
∴tanθ+
1
tanθ
的最小值是2．
点评：本题考查了基本不等式的性质和正切函数的单调性，属于基础题．
练习册系列答案
相关题目
已知数列{an}的通项公式为an=
n2-1
n2﹢1
，则从第
 
项开始，各项与1的差的绝对值小于
1
10
．
如图，海滨浴场A点处发现B点有人求救，1号救生员从A点前往营救；2号沿直线岸边向前跑到C点再前往营救；3号救生员沿直线岸边向前跑300米到离B点最近的D点再前往营救．救生员在岸边跑的速度都是6米/秒，他们水中游泳速度都是2米/秒．若∠BAD=45°，∠BCD=60°，三名救生员同时从A点出发，请说明谁先到达B点？
已知函数f（x）=-x3+3x．
（1）求函数f（x）的单调区间和极值；
（2）当x∈[0，a]，a＞0时，设f（x）的最大值是h（a），求h（a）的表达式．
已知函数y=sin（x+
π
3
）sin（x+
π
2
），求它的最大最小值，并求出取得相应最大最小值时的x值的集合．
证明：
tanα•sinα
tanα-sinα
=
tanα+sinα
tanα•sinα
．
椭圆的一焦点与两顶点为等边三角形的三个顶点，则椭圆的长轴长是短轴长的几倍．
已知向量
m
=（sin
ωx
2
，1），
n
=（
3
Acos
ωx
2
，
A
2
cosωx）（A＞0，ω＞0），函数f（x）=
m
•
n
的最大值为6，最小正周期为π．
（1）求A、ω的值；
（2）将函数y=f（x）的图象向左平移
π
2
个单位，再向上平移1个单位，得到函数y=g（x）的图象，求g（x）在[0，
5π
6
]上的值域．
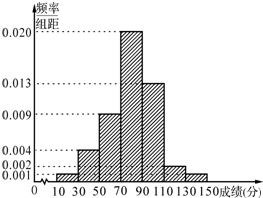某学校为了选拔学生参加“XX市中学生知识竞赛”，先在本校进行选拔测试（满分150分），若该校有100名学生参加选拔测试，并根据选拔测试成绩作出如图所示的频率分布直方图．
（Ⅰ）根据频率分布直方图，估算这100名学生参加选拔测试的平均成绩；
（Ⅱ）若通过学校选拔测试的学生将代表学校参加市知识竞赛，知识竞赛分为初赛和复赛，初赛中每人最多有5次答题机会，累计答对3题或答错3题即终止，答对3题者方可参加复赛．假设参赛者甲答对每一个题的概率都是
2
3
，求甲在初赛中答题个数的分布列和数学期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网