题目内容
12．若f（x）=（m-2）x2+2mx+1是偶函数，则f（-1），f（0），f（2）从小到大的顺序是（ ）| A． | f（0）＜f（2）＜f（1） | B． | f（-1）＜f（-2）＜f（0） | C． | f（2）＜f（-1）＜f（0） | D． | f（0）＜f（-1）＜f（2） |
分析 根据题意，由二次函数和偶函数的性质分析可得m=0，即可得函数的解析式，分析可得其在区间[0，+∞）上为减函数，比较可得0＜|-1|＜|2|，结合函数的单调性即可得答案．
解答 解：根据题意，若f（x）=（m-2）x2+2mx+1是偶函数，
则其对称轴x=-$\frac{m}{m-2}$=0，即m=0，
则函数f（x）=-2x2+1，在区间[0，+∞）上为减函数，
又由0＜|-1|＜|2|，
则f（2）＜f（-1）＜f（0）；
故选：C．
点评 本题考查函数奇偶性的性质，关键是求出m的值，确定函数单调性及单调区间．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
3．下列推理是演绎推理的是（ ）
| A． | 由圆x2+y2=r2的面积S=πr2，猜想椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的面积S=πab | |
| B． | 由金、银、铜、铁可导电，猜想：金属都可导电 | |
| C． | 猜想数列$\frac{1}{1•2}$，$\frac{1}{2•3}$，$\frac{1}{3•4}$的通项公式为an=$\frac{1}{n（n+1）}$（n∈N*） | |
| D． | 半径为r的圆的面积S=πr2，则单位圆的面积S=π |
20．${（{x-\frac{1}{x}}）^9}$的展开式中x3的系数为（ ）
| A． | -36 | B． | 36 | C． | -84 | D． | 84 |
7．函数f（x）=x3-x2-1有零点的区间是（ ）
| A． | （0，1） | B． | （-1，0） | C． | （1，2） | D． | （2，3） |
17．已知复数z=1-i，则1+z2=（ ）
| A． | 2 | B． | 1-2 | C． | 2i | D． | 1-2i |
4．已知a，b，c∈R，且a＞b，则一定成立的是（ ）
| A． | a2＞b2 | B． | $\frac{1}{a}＜\frac{1}{b}$ | C． | ac2＞bc2 | D． | $\frac{a}{{{c^2}+1}}＞\frac{b}{{{c^2}+1}}$ |
（
）.
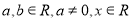的图象过点
，函数
有且只有一个零点，求
时，
是单调函数，求实数
的取值范围.