题目内容
八个一样的小球排成一排，涂上红、白两种颜色，5个涂红色，3个涂白色．若涂红色的小球恰好有三个连续，则不同涂法共有（ ）
| A、36种 | B、30种 |
| C、24种 | D、20种 |
考点：排列、组合的实际应用
专题：计算题
分析：根据题意，先把3个涂白色的小球排起来，再把3个涂红色的小球看成一体，与剩余的2个红球插入白球的空位，再分2步分析红球插入白球的情况数目，由分步计数原理计算可得答案．
解答：
解：根据题意，先把3个涂白色的小球排起来，有4个空位；
再把3个涂红色的小球看成一体，与剩余的2个红球插入白球的空位；
需要分2步分析：
①、把捆绑的小球插入3个涂白色的小球中有4种选择
②、把剩下的2个红色小球插入：2个红色小球分开有3种插法，在一起也有3种插法，
即不同的涂法有4×（3+3）=24种
故选：C．
再把3个涂红色的小球看成一体，与剩余的2个红球插入白球的空位；
需要分2步分析：
①、把捆绑的小球插入3个涂白色的小球中有4种选择
②、把剩下的2个红色小球插入：2个红色小球分开有3种插法，在一起也有3种插法，
即不同的涂法有4×（3+3）=24种
故选：C．
点评：本题考查分步计数原理的运用，注意分析题干条件，吃准“涂红色的小球恰好有三个连续”的含义．
练习册系列答案
相关题目
已知全集U={0，1，2，3，4}，集合A={1，2}，B={2，3，4}，则B∩∁UA的子集个数有（ ）
| A、2 | B、4 | C、8 | D、16 |
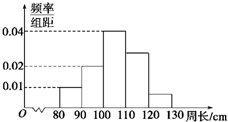为了解一片大约一万株树木的生长情况，随机测量了其中100株树木的底部周长（单位：cm）．根据所得数据画出的样本频率分布直方图如图所示，那么在这片树木中，底部周长小于110cm的株数大约是（ ）| A、3000 | B、6000 |
| C、7000 | D、8000 |
设集合S={x|x2-2x-3≤0}，T={x|-1＜x≤4，x∈Z}，则S∩T等于 （ ）
| A、{x|0＜x≤3，x∈Z} |
| B、{x|0≤x≤4，x∈Z} |
| C、{x|-1≤x≤0，x∈Z} |
| D、{x|-1＜x≤3，x∈Z} |
为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分（十进制）如图所示，假设得分值的中位数为a，众数为b，平均值为c，则（ ）| A、a=b=c |
| B、a＜c＜b |
| C、a＜b＜c |
| D、b＜a＜c |
