题目内容
6.下列命题:①a>b⇒c-a<c-b;②a>b,$c>0⇒\frac{c}{a}<\frac{c}{b}$;③a>b⇒ac2>bc2;④a3>b3⇒a>b,其中正确的命题个数是2.分析 根据不等式的性质依次判断可得结论.
解答 解:①a>b⇒-a<-b,∴c-a<c-b;不等式两边同时加减同一个数,大小不变.∴①对.
②a>b,$c>0⇒\frac{c}{a}<\frac{c}{b}$,当b<0时,不成立,②不对.
③a>b⇒ac2>bc2;当c=0时,不成立,∴③不对.
④a3>b3⇒$\root{3}{{a}^{3}}>\root{3}{{b}^{3}}$⇒a>b,∴④对.
正确的是①④.
故答案为2.
点评 本题考查了不等式的基本性质的运用.比较基础题.

练习册系列答案
相关题目
16.已知函数f(x)=ax2009+bsinx,且f(m)=2,则f(-m)=( )
| A. | 0 | B. | 1 | C. | -1 | D. | -2 |
11.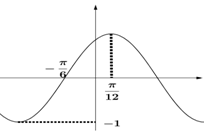 已知f(x)=Asin(ωx+φ)(A>0ω>0,$|φ|<\frac{π}{2}$,x∈R)在一个周期的图象如图所示,当$f(x)=\frac{1}{2}$时,$cos(2x-\frac{π}{6})$=( )
已知f(x)=Asin(ωx+φ)(A>0ω>0,$|φ|<\frac{π}{2}$,x∈R)在一个周期的图象如图所示,当$f(x)=\frac{1}{2}$时,$cos(2x-\frac{π}{6})$=( )
 已知f(x)=Asin(ωx+φ)(A>0ω>0,$|φ|<\frac{π}{2}$,x∈R)在一个周期的图象如图所示,当$f(x)=\frac{1}{2}$时,$cos(2x-\frac{π}{6})$=( )
已知f(x)=Asin(ωx+φ)(A>0ω>0,$|φ|<\frac{π}{2}$,x∈R)在一个周期的图象如图所示,当$f(x)=\frac{1}{2}$时,$cos(2x-\frac{π}{6})$=( )| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
15.已知$\frac{{sin2θ+2{{sin}^2}θ}}{1+tanθ}=k(\frac{π}{4}<θ<\frac{π}{2})$,则$sin(θ+\frac{π}{4})$的值( )
| A. | 随着k的增大而增大 | |
| B. | 随着k的增大而减小 | |
| C. | 是一个与k无关的常数 | |
| D. | 有时随k增大而增大,有时随k增大而减小 |
7.已知集合A={x|x2-2x>0},集合B={x|y=lg(x-1)},则A∩B=( )
| A. | (1,+∞) | B. | (2,+∞) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,0)∪(1,+∞) |
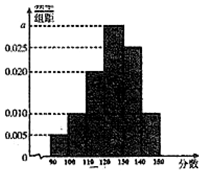 某高校从2016年招收的大一新生中,随机抽取60名学生,将他们的2016年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.
某高校从2016年招收的大一新生中,随机抽取60名学生,将他们的2016年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.