题目内容
1.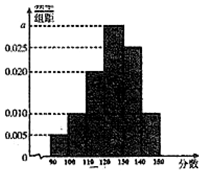 某高校从2016年招收的大一新生中,随机抽取60名学生,将他们的2016年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.
某高校从2016年招收的大一新生中,随机抽取60名学生,将他们的2016年高考数学成绩(满分150分,成绩均不低于90分的整数)分成六段[90,100),[100,110)…[140,150),后得到如图所示的频率分布直方图.(1)求图中实数a的值;
(2)若该校2016年招收的大一新生共有960人,试估计该校招收的大一新生2016年高考数学成绩不低于120分的人数;
(3)若用分层抽样的方法从数学成绩在[90,100)与[140,150]两个分数段内的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至少有1人在分数段[90,100)内的概率.
分析 (1)由频率分布直方图能求出a的值.
(2)由频率分布直方图能估计该校招收的大一新生2016年高考数学成绩不低于120分的人数.
(3)用分层抽样的方法从数学成绩在[90,100)与[140,150]两个分数段内的学生中抽取一个容量为6的样本,则数学成绩在[90,100)分数段内的学生抽取2人,数学成绩在[140,150]分数段内的学生抽取4人,至少有1人在分数段[90,100)内的对立事件是抽到的2人都在分数段[140,150]内,由此利用对立事件概率计算公式能求出至少有1人在分数段[90,100)内的概率.
解答 解:(1)由频率分布直方图得:
(0.005+0.01×2+0.02+0.025+a)×10=1,解得a=0.03(2分)
(2)由频率分布直方图估计该校招收的大一新生2015年高考数学成绩不低于1(20分)的人数为:(0.03+0.025+0.01)×10×960=624(人).(4分)
(3)用分层抽样的方法从数学成绩在[90,100)与[140,150]两个分数段内的学生中抽取一个容量为6的样本,
∵数学成绩在[90,100)分数段内的学生频率为0.005×10=0.05,
数学成绩在[140,150]分数段内的学生频率为0.010×10=0.10,
∴数学成绩在[90,100)分数段内的学生抽取2人,数学成绩在[140,150]分数段内的学生抽取4人,
∴将该样本看成一个总体,从中任取2人,基本事件总数n=15,
至少有1人在分数段[90,100)内的对立事件是抽到的2人都在分数段[140,150]内,
∴至少有1人在分数段[90,100)内的概率:P=$\frac{3}{5}$.(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案| A. | 4+$\sqrt{5}$ | B. | 4-$\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}$ |
| A. | 若q则p | B. | 若¬p则¬q | C. | 若¬q则¬p | D. | p且q |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
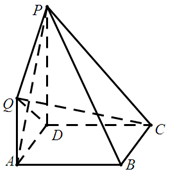 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,$QA=AB=\frac{1}{2}PD$.
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,$QA=AB=\frac{1}{2}PD$.