Question

【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，函数f（x）＝2cosxsin（x﹣A）+sinA（x∈R）在x＝处取得最大值．

（1）当时，求函数f（x）的值域；

（2）若且sinB+sinC＝，求△ABC的面积．

Answer 1

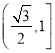【答案】（1）；（2）

【解析】

（1）化简函数，由最大值点求出A的值，注意三角形内角和.再根据三角函数性质求解取值范围.

（2）由（1）问中A的取值，再根据正弦定理，结合余弦定理，求解三角形.

∵函数

又∵函数f (x) =2cosxsin (x-A) +sinA (x∈R)在处取得最大值.

, 其中k∈z,即， 其中k∈z,

（1）

, 即函数f (x)的值域为: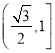

（2）由正弦定理得到，

则

即

由余弦定理得到

即

故△ABC的面积为:.