题目内容
已知集合A={x|1≤x≤3},B={x|3x>9}
(Ⅰ)分别求A∩B,(∁RB)∪A;
(Ⅱ)已知集合C={x|a-4<x<a+1},若A⊆C,求实数a的取值范围.
(Ⅰ)分别求A∩B,(∁RB)∪A;
(Ⅱ)已知集合C={x|a-4<x<a+1},若A⊆C,求实数a的取值范围.
考点:交、并、补集的混合运算
专题:集合
分析:(Ⅰ)根据集合的基本运算即可求A∩B,(CRB)∪A;
(Ⅱ)根据A⊆C,建立条件关系即可求实数a的取值范围.
(Ⅱ)根据A⊆C,建立条件关系即可求实数a的取值范围.
解答:
解:(Ⅰ)B={x|3x>9}={x|x>2},
则A∩B={x|2<x≤3},(CRB)∪A={x|1≤x≤2};
(Ⅱ)已知集合C={x|a-4<x<a+1},若A⊆C,
则
,
则
,解得1≤a≤5,
故实数a的取值范围是[1,5].
则A∩B={x|2<x≤3},(CRB)∪A={x|1≤x≤2};
(Ⅱ)已知集合C={x|a-4<x<a+1},若A⊆C,
则
|
则
|
故实数a的取值范围是[1,5].
点评:本题主要考查集合的基本运算,要求熟练掌握集合的交并补的基本运算,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个等比数列{an}共有2n+1项,奇数项之积为100,偶数项之积为120,则an+1为( )
A、
| ||
B、
| ||
| C、20 | ||
| D、110 |
若函数f(x)(x∈R)是奇函数,则( )
| A、函数f(x2)是奇函数 |
| B、函数[f(x)]2是奇函数 |
| C、函数f(x)•x2是奇函数 |
| D、函数f(x)+x2是奇函数 |
已知i是虚数单位,m和n都是实数,且m(1+i)=7+ni,则
( )
| m+ni |
| m-ni |
| A、-1 | B、1 | C、-i | D、i |
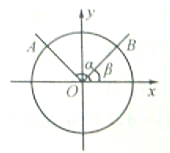 在平面直角坐标系xOy内作单位圆O,以Ox为始边作角α、β,它们的终边与单位圆O的交点为A,B,则
在平面直角坐标系xOy内作单位圆O,以Ox为始边作角α、β,它们的终边与单位圆O的交点为A,B,则