题目内容
3.在△ABC中,a,b,c分别是角A,B,C的对边,且2cosAcosC(tanAtanC-1)=1.(Ⅰ)求B的大小;
(Ⅱ)若a+c=$\sqrt{15}$,b=$\sqrt{3}$,求△ABC的面积.
分析 (Ⅰ)求出cos(A+C)=-$\frac{1}{2}$,从而求出B的大小即可;
(Ⅱ)根据余弦定理求出ac的值,从而求出三角形的面积即可.
解答 解:(Ⅰ)由2cosAcosC(tanAtanC-1)=1,
得:2cosAcosC($\frac{sinAsinC}{cosAcosC}$-1)=1,
∴2(sinAsinC-cosAcosC)=1,即cos(A+C)=-$\frac{1}{2}$,
∴cosB=-cos(A+C)=$\frac{1}{2}$,
又0<B<π,
∴B=$\frac{π}{3}$;
(Ⅱ)由b2=a2+c2-2accosB,得(a+c)2-3ac=b2,
又a+c=$\sqrt{15}$,b=$\sqrt{3}$,
∴ac=4,
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}$×4×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
点评 本题考查了余弦定理的应用,考查三角形面积公式以及三角函数求值问题,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.在国乒“直通莫斯科”比赛中共有女运动员5人,从这10名运动员中选出6人进行男女混合双打比赛,由于排名世界第一,男队的马龙,女队的丁宁自动入选,组队方案有( )
| A. | ${(A_5^2)^2}$ | B. | ${(C_4^2)^2}A_2^2$ | C. | ${(C_5^2)^2}A_3^3$ | D. | ${(C_4^2)^2}A_3^3$ |
11.若数列{an},{bn}的通项公式分别为an=(-1)n+2016•a,bn=2+$\frac{{{{(-1)}^{n+2017}}}}{n}$,且an<bn,对任意n∈N*恒成立,则实数a的取值范围是( )
| A. | $[-1,\frac{1}{2})$ | B. | [-1,1) | C. | [-2,1) | D. | $[-2,\frac{3}{2})$ |
18.已知条件p:|x+1|>2,条件q:x>a,且¬p是¬q的充分不必要条件,则a的取值范围是( )
| A. | a≤1 | B. | a≤-3 | C. | a≥-1 | D. | a≥1 |
8.执行如图所示的程序框图,如果输入n=3,则输出的S值为( )
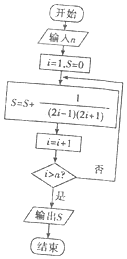

| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{7}$ | D. | $\frac{6}{7}$ |
17.已知向量$\overrightarrow a•(\overrightarrow a+2\overrightarrow b)=0$,$|\overrightarrow a|=|\overrightarrow b|=2$,则向量$\overrightarrow a,\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
18.已知角α的终边过点$P(\frac{1}{2},\frac{{\sqrt{3}}}{2})$,则sinα=( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
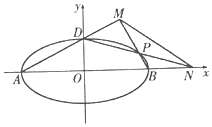 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,a+b=3.
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,a+b=3.