题目内容
4．甲、乙两队进行一场排球比赛，根据以往经验，单局比赛甲队胜乙队的概率为0.6．本场比赛采用五局三胜制，即先胜三局的队获胜，比赛结束．设各局比赛相互间没有影响，求：甲队前四局中恰好赢两局的概率．分析 直接根据独立重复试验概率公式写出结果．
解答 解：甲队前四局中恰好赢两局，其概率为P=C42（0.6）2×（0.4）2=0.3456．
点评 本题考查独立重复试验的概率公式，考查互斥事件的概率，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．已知点（x，y）满足不等式组$\left\{\begin{array}{l}{x-4y+3≤0}\\{2x-y-1≥0}\\{3x+2y-19≤0}\end{array}\right.$，则z=x-2y的最大值为（ ）
| A． | -7 | B． | -1 | C． | 1 | D． | 2 |
9．
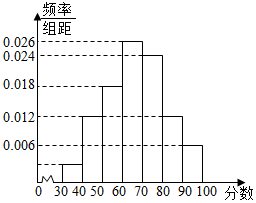某校高二年级共有1600名学生，其中男生960名，640名，该校组织了一次满分为100分的数学学业水平模拟考试，根据研究，在正式的学业水平考试中，本次成绩在[80，100]的学生可取得A等（优秀），在[60，80）的学生可取得B等（良好），在[40，60）的学生可取得C等（合格），在不到40分的学生只能取得D等（不合格），为研究这次考试成绩优秀是否与性别有关，现按性别采用分层抽样的方法抽取100名学生，将他们的成绩按从低到高分成[30，40）、[40，50）、[50，60）、[60，70）、[70，80）、[80，90）、[90，100]七组加以统计，绘制成频率分布直方图，如图是该频率分布直方图．
（Ⅰ）估计该校高二年级学生在正式的数学学业水平考试中，成绩不合格的人数；
（Ⅱ） 请你根据已知条件将下列2×2列联表补充完整，并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”？
附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$．
某校高二年级共有1600名学生，其中男生960名，640名，该校组织了一次满分为100分的数学学业水平模拟考试，根据研究，在正式的学业水平考试中，本次成绩在[80，100]的学生可取得A等（优秀），在[60，80）的学生可取得B等（良好），在[40，60）的学生可取得C等（合格），在不到40分的学生只能取得D等（不合格），为研究这次考试成绩优秀是否与性别有关，现按性别采用分层抽样的方法抽取100名学生，将他们的成绩按从低到高分成[30，40）、[40，50）、[50，60）、[60，70）、[70，80）、[80，90）、[90，100]七组加以统计，绘制成频率分布直方图，如图是该频率分布直方图．（Ⅰ）估计该校高二年级学生在正式的数学学业水平考试中，成绩不合格的人数；
（Ⅱ） 请你根据已知条件将下列2×2列联表补充完整，并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”？
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 男生 | a=12 | b= | |
| 女生 | c= | d=34 | |
| 合计 | n=100 |
| P（k2≥k0） | 0.15 | 0.10 | 0.05 |
| k0 | 2.072 | 2.706 | 3.841 |