题目内容
3.设函数f(x)=eax+λlnx,其中a<0,e是自然对数的底数(Ⅰ)若f(x)是(0,+∞)上的单调函数,求λ的取值范围;
(Ⅱ)若0<λ<$\frac{1}{e}$,证明:函数f(x)有两个极值点.
分析 (Ⅰ)求出函数的导数,通过讨论λ的范围,求出函数的单调区间,集合题意确定λ的范围即可;
(Ⅱ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而判断函数的极值点的个数.
解答 解:(Ⅰ)f′(x)=aeax+$\frac{λ}{x}$=$\frac{a{xe}^{ax}+λ}{x}$,(x>0),
①若λ≤0,则f′(x)<0,则f(x)在(0,+∞)递减,
②若λ>0,令g(x)=axeax+λ,其中a<0,x>0,
则g′(x)=aeax(1+ax),
令g′(x)=0,解得:x=-$\frac{1}{a}$,
故x∈(0,-$\frac{1}{a}$)时,g′(x)<0,g(x)递减,
x∈(-$\frac{1}{a}$,+∞)时,g′(x)>0,g(x)递增,
故x=-$\frac{1}{a}$时,g(x)取极小值也是最小值g(-$\frac{1}{a}$)=λ-$\frac{1}{e}$,
故λ-$\frac{1}{e}$≥0即λ≥$\frac{1}{e}$时,g(x)≥0,
此时f′(x)≥0,f(x)在(0,+∞)递增,
综上,所求λ的范围是(-∞,0]∪[$\frac{1}{e}$,+∞);
(Ⅱ)f′(x)=aeax+$\frac{λ}{x}$=$\frac{a{xe}^{ax}+λ}{x}$,(x>0),
令g(x)=axeax+λ,其中a<0,x>0,
求导得:g′(x)=aeax(1+ax),
令g′(x)=0,解得:x=-$\frac{1}{a}$,
x∈(0,-$\frac{1}{a}$)时,g′(x)<0,g(x)递减,
x∈(-$\frac{1}{a}$,+∞)时,g′(x)>0,g(x)递增,
x=-$\frac{1}{a}$时,g(x)取得极小值,也是最小值g(-$\frac{1}{a}$)=λ-$\frac{1}{e}$,
∵0<λ<$\frac{1}{e}$,∴g(-$\frac{1}{a}$)=λ-$\frac{1}{e}$<0,又g(0)=λ>0,
∴g(-$\frac{1}{a}$)g(0)<0,
而x→+∞时,f′(x)→λ>0,
∴函数f(x)有两个极值点.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道综合题.

| A. | 8,15,7 | B. | 16,2,2 | C. | 16,3,1 | D. | 12,5,3 |
| A. | $\frac{1}{2}{a^2}$ | B. | $\frac{1}{4}{a^2}$ | C. | $\frac{1}{8}{a^2}$ | D. | $\frac{{\sqrt{3}}}{8}{a^2}$ |
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
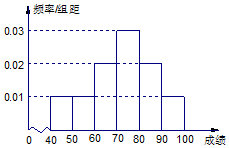 某校举办安全法规知识竞赛,从参赛的高一学生中抽出100人的成绩作为样本进行统计,并按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分组,得到成绩分布的频率分布直方图(如图).
某校举办安全法规知识竞赛,从参赛的高一学生中抽出100人的成绩作为样本进行统计,并按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分组,得到成绩分布的频率分布直方图(如图).