题目内容
13．设集合A={x|-1＜x≤2}，Z为整数集，则集合A∩Z中元素的个数是（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
分析 求出A与Z的交集，即可作出判断．
解答 解：∵A={x|-1＜x≤2}，Z为整数集，
∴A∩Z={0，1，2}，
则集合A∩Z中元素的个数是3，
故选：A．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
4．已知向量$\overrightarrow a=（\;t，\;1）$和$\overrightarrow b=（-2，\;t+2）$，若$\overrightarrow a⊥\overrightarrow b$，则$|\overrightarrow a+\overrightarrow b|$=（ ）
| A． | 64 | B． | 8 | C． | 5 | D． | $\sqrt{10}$ |
8．已知x1＞0，x2＞0，x1+x2＜ex1x2（e为自然对数的底数），则（ ）
| A． | x1+x2＞1 | B． | x1+x2＜1 | C． | $\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$＜$\frac{1}{e}$ | D． | $\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$＞$\frac{1}{e}$ |
18．若复数z满足$z=\frac{2+i}{i}$（其中i为虚数单位），则$\overline z$=（ ）
| A． | -1+2i | B． | -1-2i | C． | 1-2i | D． | 1+2i |
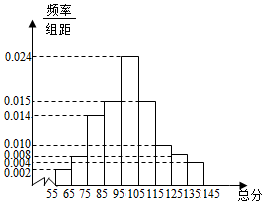从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本，分别统计出这些试卷总分，由总分得到如下的频率分布直方图．
8．复数$\frac{{i（{-6+i}）}}{{|{3-4i}|}}$的实部与虚部之差为（ ）
| A． | -1 | B． | 1 | C． | $-\frac{7}{5}$ | D． | $\frac{7}{5}$ |