题目内容
 如图是一个几何体的三视图,正视图中实线段构成的矩形的长为4,宽为2;俯视图为同心圆,且内圆直径为2,则这个几何体的体积为
如图是一个几何体的三视图,正视图中实线段构成的矩形的长为4,宽为2;俯视图为同心圆,且内圆直径为2,则这个几何体的体积为考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:利用几何体的三视图判断襟怀坦荡形状,通过三视图的数据,求出几何体的体积.
解答:
解:由几何体的三视图可知,几何体是圆柱中间去掉一个同轴的小圆柱的几何体,
圆柱的高为2,底面半径分别为2,1.
∴圆柱的体积为:22×2π-12×2π=6π.
故答案为:6π.
圆柱的高为2,底面半径分别为2,1.
∴圆柱的体积为:22×2π-12×2π=6π.
故答案为:6π.
点评:本题考查几何体的三视图的体积与表面积的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
设A(3,2,1),B(1,0,5),C(0,2,1),AB的中点为M,则|CM|=( )
| A、3 | ||
B、
| ||
C、2
| ||
D、3
|
过椭圆C:
+
=1上任一点P,作椭圆C的右准线的垂线PH(H为垂足),延长PH到点Q,使|HQ|=λ|PH|(λ≥1).当点P在椭圆C上运动时,点Q的轨迹的离心率的取值范围为( )
| x2 |
| 3 |
| y2 |
| 2 |
A、(0,
| ||||||||
B、(
| ||||||||
C、[
| ||||||||
D、(
|
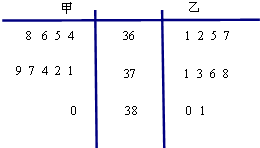 学校为了预防甲流感,每天上午都要对同学进行体温抽查.某一天,随机抽取甲、乙两个班级各10名同学,测量他们的体温如图:(单位0.1℃)
学校为了预防甲流感,每天上午都要对同学进行体温抽查.某一天,随机抽取甲、乙两个班级各10名同学,测量他们的体温如图:(单位0.1℃)