题目内容
7．若圆C经过坐标原点，且圆心在直线y=-2x+3上运动，求当半径最小时圆的方程．分析 设圆心（a，-2a+3），利用二次函数的性质求得圆的半径的最小值以及此时圆心的坐标，从而得到当半径最小时圆的方程．
解答 解：设圆心（a，-2a+3），则半径为r=$\sqrt{{a}^{2}{+（-2a+3）}^{2}}$=$\sqrt{{5a}^{2}-12a+9}$，
故当a=$\frac{6}{5}$时，r取得最小值为$\frac{3\sqrt{5}}{5}$，故当半径最小时圆的方程为 ${（x-\frac{6}{5}）}^{2}$+${（y-\frac{3}{5}）}^{2}$=$\frac{9}{5}$．
点评 本题主要考查求圆的标准方程的方法，二次函数的性质，属于基础题．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
17．若实数x，y满足不等式组$\left\{\begin{array}{l}{|x-1|≤1}\\{y≥0}\\{y≤x+1}\end{array}\right.$，则下列结论中正确的是（ ）
| A． | 2x-y≥0 | B． | 2x-y≤3 | C． | x+y≤6 | D． | x+y＜2 |
2．圆x2+y2-2x-2y+1=0的圆心到直线x-y-2=0的距离为（ ）
| A． | $\sqrt{2}$ | B． | 2$\sqrt{2}$ | C． | 3$\sqrt{2}$ | D． | 0 |
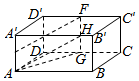已知长方体ABCD-A1B1C1D1，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$，E，F分别为AA1，C1D1中点，则$\overrightarrow{EF}$可用$\vec a，\vec b，\vec c$表示为$\frac{1}{2}$（$\overrightarrow{a}$+$\overrightarrow{c}$）+$\overrightarrow{b}$．