题目内容
10．经过两点A（4，2y+1），B（2，-3）的直线的倾斜角为45°，则y的值为（ ）| A． | -1 | B． | -3 | C． | 0 | D． | 2 |
分析 由两点坐标求出直线的斜率，再由斜率等于倾斜角的正切值列式求得y的值．
解答 解：经过两点A（4，2y+1），B（2，-3）的直线的斜率为k=$\frac{-3-2y-1}{2-4}=y+2$．
又直线的倾斜角为45°，
∴y+2=tan45°=1，即y=-1．
故选：A．
点评 本题考查直线的倾斜角，考查了直线倾斜角与斜率的关系，是基础题．
练习册系列答案
相关题目
11．如图，是函数y=f（x）=sin（ω1x+φ1）和y=g（x）=sin（ω2x+φ2）在一个周期上的图象，为了得到y=f（x）的图象，只要将y=g（x）的图象上所有的点（ ）
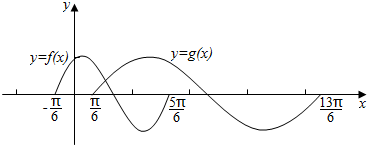
| A． | 向左平移$\frac{π}{3}$个单位长度．再把所得点的横坐标伸长到原来的2倍．纵坐标不变 | |
| B． | 向左平移$\frac{π}{3}$个单位长度．再把所得点的横坐标缩短到原来的$\frac{1}{2}$倍．纵坐标不变 | |
| C． | 向左平移$\frac{π}{2}$个单位长度．再把所得点的横坐标伸长到原来的2倍．纵坐标不变 | |
| D． | 向左平移$\frac{π}{2}$个单位长度．再把所得点的横坐标缩短到原来的$\frac{1}{2}$倍．纵坐标不变 |
8．在半径为R的球内放入5个球，其中有4个球大小相等，两两相外切且均与大球相内切，另一个小球与这四个球均相外切，则这个小球半径为（ ）
| A． | （3-2$\sqrt{2}$）R | B． | （4-2$\sqrt{3}$）R | C． | （5-2$\sqrt{6}$）R | D． | （6-2$\sqrt{7}$）R |
5．已知函数f（x）是定义在R上的偶函数，当x∈[0，+∞）时，f（x）是增函数，且f（-1）=0则不等式f（x）＜0的解集为（ ）
| A． | （-1，1） | B． | （-∞，-1）∪（1，+∞） | C． | （-∞，-1）∪（0，1） | D． | （-1，0）∪（0，1） |
20．
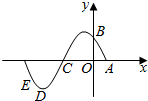已知A，B，C，D是函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）一个周期内的图象上的四个点，如图所示，$A（\frac{π}{6}，0）$，B为y轴上的点，D为图象上的最低点，C为该函数图象的一个对称中心，B与E关于点C对称，$\overrightarrow{ED}$在x轴上的投影为$\frac{π}{12}$，则$f（-\frac{π}{6}）$的值为（ ）
已知A，B，C，D是函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）一个周期内的图象上的四个点，如图所示，$A（\frac{π}{6}，0）$，B为y轴上的点，D为图象上的最低点，C为该函数图象的一个对称中心，B与E关于点C对称，$\overrightarrow{ED}$在x轴上的投影为$\frac{π}{12}$，则$f（-\frac{π}{6}）$的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $-\frac{1}{2}$ | D． | $-\frac{{\sqrt{3}}}{2}$ |