题目内容
设抛物线C:y2=2px(p>0)的焦点为F,准线为l,l与x轴交于点R,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.
(1)若∠BFD=120°,△ABD的面积为8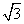 ,求p的值及圆F的方程;
,求p的值及圆F的方程;
(2)在(1)的条件下,若A,B,F三点在同一直线上,FD与抛物线C交于点E,求△EDA的面积.
解:(1)因为∠BFD=120°,|BF|=|FD|,
所以∠FBD=∠FDB=30°,
在Rt△BRF中,因为|FR|=p,
所以|BF|=2p,|BR|=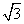 p.
p.
在Rt△DRF中,同理有|DF|=2p,|DR|=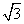 p,
p,
所以|BD|=|BR|+|RD|=2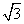 p,
p,
圆F的半径|FA|=|FB|=2p.
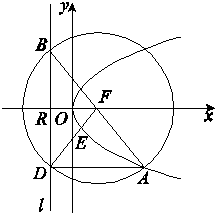
由抛物线定义可知,A到l的距离d=|FA|=2p,
因为△ABD的面积为8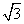 ,
,
所以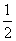 |BD|·d=8
|BD|·d=8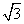 ,
,
即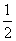 ×2
×2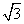 p×2p=8
p×2p=8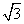 ,解得p=-2(舍去)或p=2,所以F(1,0),圆F的方程为(x-1)2+y2=16.
,解得p=-2(舍去)或p=2,所以F(1,0),圆F的方程为(x-1)2+y2=16.
(2)因为A,B,F三点在同一直线上,所以AB为圆F的直径,∠ADB=90°,
由抛物线定义知,|AD|=|FA|=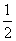 |AB|,所以∠ABD=30°,
|AB|,所以∠ABD=30°,
直线DF的斜率k=tan 60°=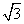 ,其方程为y=
,其方程为y=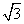 (x-1),
(x-1),
解方程组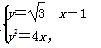 得
得
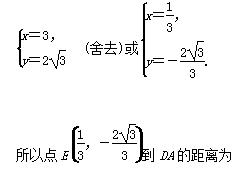 d′=|DR|-|yE|=2
d′=|DR|-|yE|=2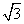 -
- =
=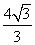 ,
,
所以S△EDA=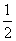 |DA|·d′=
|DA|·d′=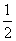 ×4×
×4×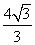 =
=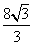 .
.

练习册系列答案
相关题目
 均是实数,则
均是实数,则 的 ( )
的 ( ) .充分非必要条件 B.必要非充分条件
.充分非必要条件 B.必要非充分条件  国家规定个人稿费纳税办法是:不超过800元的不纳税;超过800元而不超过4000元的按超过800元部分14%的纳税;超过4000元的按全部稿酬的11%纳税。已知某人出版一本书,共纳税420元,这个人应得稿费(扣税前)为 元。
国家规定个人稿费纳税办法是:不超过800元的不纳税;超过800元而不超过4000元的按超过800元部分14%的纳税;超过4000元的按全部稿酬的11%纳税。已知某人出版一本书,共纳税420元,这个人应得稿费(扣税前)为 元。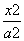 -
-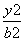 =1(a>0,b>0)与抛物线y2=2px(p>0)的交点为A,B,A,B连线经过抛物线的焦点F,且线段AB的长等于双曲线的虚轴长,则双曲线的离心率为( )
=1(a>0,b>0)与抛物线y2=2px(p>0)的交点为A,B,A,B连线经过抛物线的焦点F,且线段AB的长等于双曲线的虚轴长,则双曲线的离心率为( )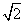 B.2 C.3 D.
B.2 C.3 D.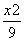 -
-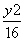 =1的一个顶点和一个焦点,圆心M在双曲线S上,则圆心M到双曲线S的中心的距离为________.
=1的一个顶点和一个焦点,圆心M在双曲线S上,则圆心M到双曲线S的中心的距离为________.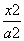 -
-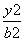 =1(a>0,b>0)的左、右焦点分别为F1,F2,点O为坐标原点,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则|OA|与|OB|的长度依次为( )
=1(a>0,b>0)的左、右焦点分别为F1,F2,点O为坐标原点,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则|OA|与|OB|的长度依次为( )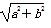
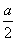 ,
,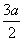 D.
D.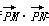 =2b2,则该双曲线的离心率为( )
=2b2,则该双曲线的离心率为( )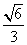 B.
B.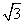 C.
C. D.
D.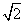
 -3的两个零点,若a<x1<x2,则f(a)的值满足( )
-3的两个零点,若a<x1<x2,则f(a)的值满足( ) 中,内角
中,内角 的对应边分别为
的对应边分别为 ,向量
,向量 与
与 平行. (Ⅰ)求角
平行. (Ⅰ)求角 的值; (Ⅱ)若
的值; (Ⅱ)若 ,求
,求