题目内容
20．已知物体的运动方程为s=$\frac{1}{4}{t^4}-4{t^3}+16{t^2}$（t表示时间，单位：秒；s表示位移，单位：米），则瞬时速度为0米每秒的时刻是（ ）| A． | 0秒、2秒或4秒 | B． | 0秒、2秒或16秒 | C． | 0秒、4秒或8秒 | D． | 2秒、8秒或16秒 |
分析 对物体的运动方程求导为瞬时速度，令其为0得瞬时速度为0米每秒的时刻．
解答 解：s′=t3-12t2+32t
令s′=t3-12t2+32t=0得
t=0或 t=4或t=8
故选：C．
点评 考查导数在物理中的应用：位移求导为瞬时速度．
练习册系列答案
相关题目
11．探究函数$f（x）=2x+\frac{8}{x}，x∈（0，+∞）$的最小值，并确定取得最小值时x的值．列表如下：
请观察表中y值随x值变化的特点，完成以下的问题．
（1）函数$f（x）=2x+\frac{8}{x}（x＞0）$在区间（0，2）上递减；函数$f（x）=2x+\frac{8}{x}（x＞0）$在区间（2，+∞）上递增．当x=2时，y最小=8．
（2）证明：函数$f（x）=2x+\frac{8}{x}（x＞0）$在区间（0，2）递减．
（3）思考：函数y=2x+$\frac{8}{x}$时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 16 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | … |
（1）函数$f（x）=2x+\frac{8}{x}（x＞0）$在区间（0，2）上递减；函数$f（x）=2x+\frac{8}{x}（x＞0）$在区间（2，+∞）上递增．当x=2时，y最小=8．
（2）证明：函数$f（x）=2x+\frac{8}{x}（x＞0）$在区间（0，2）递减．
（3）思考：函数y=2x+$\frac{8}{x}$时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）
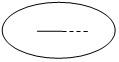
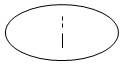
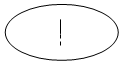
日晷，是中国古代利用日影测得时刻的一种计时工具，又称“日规”．其原理就是利用太阳的投影方向来测定并划分时刻．利用日晷计时的方法是人类在天文计时领域的重大发明，这项发明被人类沿用达几千年之久．如图是故宫中的一个日晷，则根据图片判断此日晷的侧（左）视图可能为 （ ）
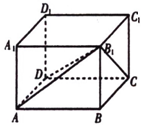在长方体ABCD-A1B1C1D1任意取点，则该点落在四棱锥B1-ABCD内部的概率是$\frac{1}{3}$．
10．已知$\frac{m}{1-i}=1+ni$，其中m、n是实数，i是虚数单位，则m+ni=（ ）
| A． | 1+2i | B． | 1-2i | C． | 2+i | D． | 2-i |