题目内容

1．两圆C1：x2+y2-4x+3=0和C2：${x^2}+{y^2}+4\sqrt{3}y+3=0$的位置关系是（　　）
A．相离B．相交C．内切D．外切

分析 根据两圆的圆心距与两个圆的半径和的关系，可得两圆的位置关系．

解答 解：由题意可得，圆C2：x2+y2-4x+3=0可化为（x-2）2+y2=1，
C2：${x^2}+{y^2}+4\sqrt{3}y+3=0$的x2+（y+2$\sqrt{3}$）2=9
两圆的圆心距C1C2=$\sqrt{（{2-0）}^{2}+（0-2\sqrt{3}）^{2}}$=4=1+3，
∴两圆相外切．
故选：D．

点评 本题主要考查圆的标准方程，两个圆的位置关系的判定方法，属于中档题．

练习册系列答案
相关题目
11．若f（x）=$\frac{1}{{x}^{2}-2ax+a+5}$在（-2，2）上单调递增，则a的取值范围是[2，3]．
12．设α，β是两个不同的平面，直线m⊥α，则“m⊥β”是“α∥β”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
9．已知数列{an}与{bn}满足an+1-an=2（bn+1-bn）（n∈N*）．
（1）若a1=1，bn=3n+5，求数列{an}的通项公式；
（2）若a1=6，bn=2n（n∈N*）且λan＞2n+n+2λ对一切n∈N*恒成立，求实数λ的取值范围．
16．设{an}是公比为q的等比数列．
（Ⅰ）推导{an}的前n项和Sn公式；
（Ⅱ）设q≠1，证明数列$\left\{{\frac{S_n}{n}}\right\}$不是等比数列．
6．在平面直角坐标系xOy中，已知圆C：（x-3）2+y2=4，点A，B在圆C上，且$|{AB}|=2\sqrt{3}$，则$|{\overrightarrow{OA}+\overrightarrow{OB}}|$的最大值是（　　）
A．8B．$4\sqrt{2}$C．4D．$2\sqrt{2}$
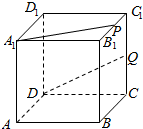13．如图，在正方体ABCD-A1B1C1D1中，点P、Q分别是B1C1、CC1的中点，则直线A1P与DQ的位置关系是相交．（填“平行”、“相交”或“异面”）
10．已知二次函数f（x）有两个零点-3和1，且有最小值-4．
（Ⅰ） 求f（x）的解析式；
（Ⅱ） 令g（x）=mf（x）+1（m≠0）．
①若m＜0，证明：g（x）在[-3，+∞）上有唯一零点；
②若m＞0，求y=|g（x）|在$[{-3，\frac{3}{2}}]$上的最大值．
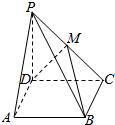11．已知四棱锥P-ABCD的底面是平行四边形，如图，M是PC的中点，问向量$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$是否可以组成一个基底，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网