题目内容
设各项均为正数的数列{an}的前n项和为Sn,满足4Sn=an+12-4n-1,n∈N*,且a2,a5,a14恰为等比数列{bn}的前三项.
(Ⅰ)证明:数列{an}为等差数列;
(Ⅱ)求数列{an•bn}的前n项和Tn.
(Ⅰ)证明:数列{an}为等差数列;
(Ⅱ)求数列{an•bn}的前n项和Tn.
考点:数列的求和,等差关系的确定
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件推导出
=(an+2)2,由此能够证明{an}为首项是1,公差为2的等差数列.
(Ⅱ)an=2n-1,bn=3n,利用错位相减求和法能求出数列{an•bn}的前n项和Tn.
| a | 2 n+1 |
(Ⅱ)an=2n-1,bn=3n,利用错位相减求和法能求出数列{an•bn}的前n项和Tn.
解答:
(Ⅰ)证明:当n≥2时,4Sn-1=
-4(n-1)-1,
∴4an=4Sn-4Sn-1=
-
-4,
∴
=(an+2)2,∵an>0,∴an+1=an+2,…(2分)
∴n≥2时,{an}为公差为2的等差数列,
∴a2,a5,a14恰为等比数列{bn}的前三项,
∴a52=a2a14,
即(a2+6)2=a2(a2+24),解得a2=3,…(3分)
由条件知4a1=a22-5,则a1=1,…(4分)
∴a2-a1=2=an+1-an,
∴{an}为首项是1,公差为2的等差数列.…(6分)
(Ⅱ)解:由(Ⅰ)知an=2n-1,bn=3n,…(8分)
∴Tn=1×3+3×32+5×33+…+(2n-1)3n,
两边同乘以3得,3Tn=1×32+3×33+…+(2n-3)3n+(2n-1)3n+1,…(9分)
两式相减得-2Tn=1×3+2(32+33+…+3n)-(2n-1)3n+1
=3+2
-(2n-1)3n+1=-6+(2-2n)3n+1,…(12分)
∴Tn=3+(n-1)3n+1.…(13分)
| a | 2 n |
∴4an=4Sn-4Sn-1=
| a | 2 n+1 |
| a | 2 n |
∴
| a | 2 n+1 |
∴n≥2时,{an}为公差为2的等差数列,
∴a2,a5,a14恰为等比数列{bn}的前三项,
∴a52=a2a14,
即(a2+6)2=a2(a2+24),解得a2=3,…(3分)
由条件知4a1=a22-5,则a1=1,…(4分)
∴a2-a1=2=an+1-an,
∴{an}为首项是1,公差为2的等差数列.…(6分)
(Ⅱ)解:由(Ⅰ)知an=2n-1,bn=3n,…(8分)
∴Tn=1×3+3×32+5×33+…+(2n-1)3n,
两边同乘以3得,3Tn=1×32+3×33+…+(2n-3)3n+(2n-1)3n+1,…(9分)
两式相减得-2Tn=1×3+2(32+33+…+3n)-(2n-1)3n+1
=3+2
| 32(1-3n-1) |
| 1-3 |
∴Tn=3+(n-1)3n+1.…(13分)
点评:本题考查等差数列的证明,考查数列的前n项和的求法,解题时要认真审题,注意错位相减求和法的合理运用.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
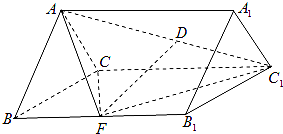 如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1.
如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1. 如图,四棱柱ABCD-A1B1C1D1中,平面A1ABB1⊥平面ABCD,且∠ABC=
如图,四棱柱ABCD-A1B1C1D1中,平面A1ABB1⊥平面ABCD,且∠ABC=