题目内容
 长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,AA1=4.
长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,AA1=4.(1)说出BD1与平面BCC1B1所成角,并求出它的余弦值;
(2)指出二面角D1-AC-D的平面角,并求出它的正切值;
(3)求该长方体的外接球的表面积.
考点:棱柱、棱锥、棱台的体积,直线与平面所成的角,二面角的平面角及求法
专题:空间位置关系与距离
分析:(1)连结BC1,则∠D1BC1就是BD1与平面BCC1B1所成角,由此能求出BD1与平面BCC1B1所成角的余弦值.(2)连结AC,BD,交于O,连结OD1,则∠DOD1是二面角D1-AC-D的平面角,由此能求出二面角D1-AC-D的正切值.
(3)该长方体的外接球半径R=
=
,由此能求出该长方体的外接球的表面积.
(3)该长方体的外接球半径R=
| 1 |
| 2 |
| 4+4+16 |
| 6 |
解答:
解:(1)连结BC1,则∠D1BC1就是BD1与平面BCC1B1所成角,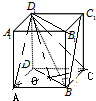
∵长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,AA1=4,
∴BC1=
=2
,BD1=
=2
,
∴cos∠D1BC1=
=
=
.
∴BD1与平面BCC1B1所成角的余弦值为
.
(2)连结AC,BD,交于O,连结OD1,
则∠DOD1是二面角D1-AC-D的平面角,
∵DD1=4,OD=
,
∴tan∠DOD1=
=
=2
.
∴二面角D1-AC-D的正切值为2
.
(3)该长方体的外接球半径R=
=
,
∴该长方体的外接球的表面积S=4π×(
)2=24π.

∵长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,AA1=4,
∴BC1=
| 4+16 |
| 5 |
| 4+4+16 |
| 6 |
∴cos∠D1BC1=
| BC1 |
| BD1 |
2
| ||
2
|
| ||
| 6 |
∴BD1与平面BCC1B1所成角的余弦值为
| ||
| 6 |
(2)连结AC,BD,交于O,连结OD1,
则∠DOD1是二面角D1-AC-D的平面角,
∵DD1=4,OD=
| 2 |
∴tan∠DOD1=
| DD1 |
| DO |
| 4 | ||
|
| 2 |
∴二面角D1-AC-D的正切值为2
| 2 |
(3)该长方体的外接球半径R=
| 1 |
| 2 |
| 4+4+16 |
| 6 |
∴该长方体的外接球的表面积S=4π×(
| 6 |
点评:本题考查二面角的余弦值和正切值的求法,考查长方体的外接球的表面积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目