Question

19．已知点A，B，C在球O的表面上且A=$\frac{π}{3}$，b=1，c=3．三菱锥O-ABC的体积为$\frac{\sqrt{2}}{2}$，则球O的表面积为（　　）

• A． 16π
• B． 32π
• C． 20π
• D． 5π

Answer 1

分析 利用解三角形得出截面圆的半径r，利用d²+r²=R²，求解R，计算球的表面积．

解答 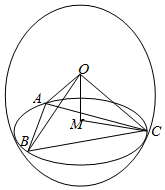解：在△ABC中，由a²=b²+c²-2bccosA得a=$\sqrt{7}$
设△ABC的外接圆的圆心为r，则2r=$\frac{\sqrt{7}}{sin\frac{π}{3}}$，即r=$\frac{\sqrt{7}}{\sqrt{3}}$
∵三菱锥O-ABC的体积为$\frac{\sqrt{2}}{2}$，∴$\frac{1}{3}×\frac{1}{2}×3×1×sin\frac{π}{3}$×h=$\frac{\sqrt{2}}{2}$
∴O到平面ABC的距离h=$\frac{2\sqrt{6}}{3}$
∴球O的半径为R=$\sqrt{{h}^{2}+{r}^{2}}$=$\sqrt{5}$．
∴则球O的表面积为4πR²=20π
故选：C

点评 本题综合考察了学生的空间思维能力，空间几何体性质，利用平面问题解决空间几何问题，属于中档题．