Question

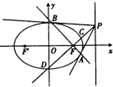已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

1

2

，以原点为圆心，以椭圆的短半轴长为半径的圆与直线x-y+

6

=0相切．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过椭圆的右焦点F的直线l₁与椭圆交于A、B，过F与直线l₁垂直的直线l₂与椭圆交于C、D，与直线l₂：x=4交于P．
①求四边形ABCD面积的最小值；
②求证：直线PA，PF，PB的斜率k_PA，k_PF，k_PB成等差数列．

Answer 1

考点：直线与圆锥曲线的关系,等差数列的通项公式,直线的斜率,椭圆的标准方程

专题：综合题,圆锥曲线的定义、性质与方程

分析：（Ⅰ）椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

1

2

，可得a²=

4

3

b²，利用椭圆的短半轴为半径的圆与直线x-y+

6

=0相切，求出b，即可求椭圆C的方程；
（Ⅱ）①分类讨论，设出方程代入椭圆方程，利用基本不等式，即可求四边形ABCD面积的最小值；
②分类讨论，设出方程，证明k_PA+k_PB=2k_PF，即可证明直线PA，PF，PB的斜率k_PA，k_PF，k_PB成等差数列．

解答： 解：（Ⅰ）∵椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

1

2

，
∴

a2-b2

a2

=

1

4

，∴a²=

4

3

b²，
∵椭圆的短半轴为半径的圆与直线x-y+

6

=0相切．
∴b=

6

12+(-1)2

=

3

，
∴a²=4，b²=3
∴椭圆的方程为

x2

4

+

y2

3

=1；
（Ⅱ）①斜率不存在时，方程为x=1，
代入椭圆方程可得y=±

3

2

，
∴|AB|=3，|CD|=2a=4，
∴四边形ABCD面积为

1

2

×3×4=6；
斜率不为0时，方程为y=k（x-1），
代入椭圆方程可得（4k²+3）x²-8k²x+4k²-12=0
设A（x₁，y₁），B（x₂，y₂），则x₁+x₂=

8k2

4k2+3

，x₁x₂=

4k2-12

4k2+3

，
∴|AB|=

1+k2

|x₁-x₂|=

12(1+k2)

3+4k2

，
同理|CD|=

12(1+k2)

4+3k2

，
∴

1

|AB|

+

1

|CD|

=

12(1+k2)

3+4k2

+

12(1+k2)

4+3k2

=

7

12

≥2

1 |AB||CD|

，
∴|AB||CD|≥

122×4

49

，
∴S_ABCD=

1

2

|AB||CD|≥

1

2

×

122×4

49

=

288

49

，
∵

288

49

＜6，
∴四边形ABCD面积的最小值为

288

49

；
②l₁的斜率存在时，则直线l₂的方程为y=-

1

k

（x-1）．
令x=4，则P（4，-

3

k

），
∴k_PA+k_PB=

y1+ 3 k

x1-4

+

y2+ 3 k

x2-4

=

k(x1-1)

x1-4

+

k(x2-1)

x2-4

+

3

k

×

x1+x2-8

(x1-4)(x2-4)

=-

2

k

=2k_PF．
l₁的斜率不存在时，由对称性知，k_PA+k_PB=2k_PF．
∴直线PA，PF，PB的斜率k_PA，k_PF，k_PB成等差数列．

点评：本题考查椭圆方程，考查直线与椭圆的位置关系，考查分类讨论的数学思想，属于难题．