题目内容
在平面直角坐标系中,已知三点A(m,n),B(n,t),C(t,m),直线AC的斜率与倾斜角为钝角的直线AB的斜率之和为
,而直线AB恰好经过抛物线x2=2p(y-q),(p>0)的焦点F并且与抛物线交于P、Q两点(P在y轴左侧).则|
|=( )
| 5 |
| 3 |
| PF |
| QF |
| A、9 | ||||
| B、4 | ||||
C、
| ||||
D、
|
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先设出直线AB,AC的斜率,利用已知条件建立等式求得直线AB的斜率,进而利用点斜式表示出直线AB的方程,与抛物线方程联立,求得关于x的方程,求得P,Q的坐标,进而利用斜率和横坐标分别表示出|PF|,|QF|,最后求得其比值.
解答:
解:设kAB=
,kAC=
,
则
+
=
,
∵(n-m)•kAB=t-n=(t-m)+(m-n),
∴
=-
,
∴kAB-
=
,解得kAB=-
或2(舍去),
∵直线AB过抛物线x2=2p(y-q)的焦点,和直线AB过抛物线x2=2py的焦点,对|
|的值没有影响,故可研究AB过抛物线x2=2py的情况,
∴直线AB的方程为y=-
x+
,与抛物线联立消去y,
整理得x2+
x-p2=0,求得x=-
或
.
∵抛物线x2=2py的焦点为(0,
),设P(x1,y1),Q(x2,y2),P在y轴左侧,
∴x1=-
,x2=
∴|PF|=
(|x1-0|)=
|x1|,|QF|=
(|x1-0|)=
x2,
∴|
|=|
|=|
|=|
|=9.
故选:A.
| t-n |
| n-m |
| m-n |
| t-m |
则
| t-n |
| n-m |
| m-n |
| t-m |
| 5 |
| 3 |
∵(n-m)•kAB=t-n=(t-m)+(m-n),
∴
| m-n |
| t-m |
| 1 |
| kAB+1 |
∴kAB-
| 1 |
| kAB+1 |
| 5 |
| 3 |
| 4 |
| 3 |
∵直线AB过抛物线x2=2p(y-q)的焦点,和直线AB过抛物线x2=2py的焦点,对|
| PF |
| QF |
∴直线AB的方程为y=-
| 4 |
| 3 |
| p |
| 2 |
整理得x2+
| 8p |
| 3 |
| 9p |
| 3 |
| p |
| 3 |
∵抛物线x2=2py的焦点为(0,
| p |
| 2 |
∴x1=-
| 9p |
| 3 |
| p |
| 3 |
∴|PF|=
| 1+k2 |
| 1+k2 |
| 1+k2 |
| 1+k2 |
∴|
| PF |
| QF |
| ||
|
| x1 |
| x2 |
-
| ||
|
故选:A.
点评:本题主要考查了直线与圆锥曲线的位置关系.一般思路是直线方程与抛物线方程联立,消去x或y,转化为一元二次方程的问题,找到问题的突破口.

练习册系列答案
相关题目
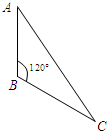 在△ABC中,AB=3,BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,则所形成的几何体的体积是( )
在△ABC中,AB=3,BC=4,∠ABC=120°,若把△ABC绕直线AB旋转一周,则所形成的几何体的体积是( )| A、11π | B、12π |
| C、13π | D、14π |
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、1 | ||
B、
| ||
C、
| ||
D、
|
cos600°=( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知
=(1,2,-1),则向量
的模的大小为( )
| a |
| a |
| A、4 | ||
| B、6 | ||
C、
| ||
D、
|
复数(1-i)2的虚部是( )
| A、-2i | B、2 | C、-2 | D、0 |
定义域为R的四个函数y=x2+1,y=3x,y=|x+1|,y=sinx中,偶函数的个数是( )
| A、4 | B、3 | C、2 | D、1 |