题目内容
已知双曲线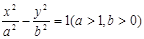 的焦距为2c,离心率为e,若点(-1,0)与点(1,0)到直线
的焦距为2c,离心率为e,若点(-1,0)与点(1,0)到直线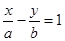 的距离之和为S,且S
的距离之和为S,且S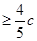 ,则离心率e的取值范围是( )
,则离心率e的取值范围是( )
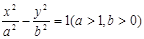 的焦距为2c,离心率为e,若点(-1,0)与点(1,0)到直线
的焦距为2c,离心率为e,若点(-1,0)与点(1,0)到直线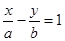 的距离之和为S,且S
的距离之和为S,且S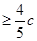 ,则离心率e的取值范围是( )
,则离心率e的取值范围是( )A. | B. | C. | D. |
A
解:直线l的方程为 xa+yb=1,即bx+ay-ab=0.
由点到直线的距离公式,且a>1,得到点(1,0)到直线l的距离 ,
,
同理得到点(-1,0)到直线l的距离.d2= ,s=d1+d2=
,s=d1+d2=
由S≥4 /5 c,得5 c2-a2≥2c2.于是得4e4-25e2+25≤0.解不等式,得 5 /4 ≤e 2≤5.由于e>1>0,所以e的取值范围是 e∈[ ,
,  ].故选A.
].故选A.
由点到直线的距离公式,且a>1,得到点(1,0)到直线l的距离
 ,
,同理得到点(-1,0)到直线l的距离.d2=
 ,s=d1+d2=
,s=d1+d2=
由S≥4 /5 c,得5 c2-a2≥2c2.于是得4e4-25e2+25≤0.解不等式,得 5 /4 ≤e 2≤5.由于e>1>0,所以e的取值范围是 e∈[
 ,
,  ].故选A.
].故选A.
练习册系列答案
相关题目
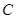 :
: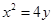 ,过点
,过点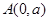 (其中
(其中 为正常数)任意作一条直线
为正常数)任意作一条直线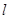 交抛物线
交抛物线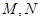 两点,
两点,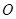 为坐标原点.
为坐标原点.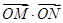 的值;
的值;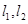 ,试探求
,试探求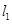 与
与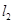 的交点是否在定直线上,证明你的结论.
的交点是否在定直线上,证明你的结论. 的双曲线的标准方程为 。
的双曲线的标准方程为 。 的右支上存在一点,它到右焦点及左准线的距离相等,则双曲线离心率的取值范围是 ( )
的右支上存在一点,它到右焦点及左准线的距离相等,则双曲线离心率的取值范围是 ( )



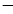 y2 =1,点F1,F2为其两个焦点,点P为双曲线上一点,若P F1⊥PF2,则∣P F1∣+∣P F2∣的值为___________________.
y2 =1,点F1,F2为其两个焦点,点P为双曲线上一点,若P F1⊥PF2,则∣P F1∣+∣P F2∣的值为___________________. (a>0,b>0)与抛物线y2=8x有一个公共的焦点F,两曲线的一个交点为P.若|PF|=5,则双曲线的渐近线方程为____.
(a>0,b>0)与抛物线y2=8x有一个公共的焦点F,两曲线的一个交点为P.若|PF|=5,则双曲线的渐近线方程为____. 的焦点为F1、F2,点M在双曲线上,且
的焦点为F1、F2,点M在双曲线上,且 轴,则F1到F2M距离是( ).
轴,则F1到F2M距离是( ).



 的左焦点
的左焦点 引圆
引圆 的切线
的切线 ,交双曲线的右支于点
,交双曲线的右支于点 ,
, 为切点,
为切点, 为线段
为线段 是坐标原点,则
是坐标原点,则 等于( )
等于( )


