题目内容
已知椭圆
+
=1(a>b>0)的两个焦点为F1、F2,以F1F2为直径的圆与椭圆交于点P,若△F1PF2的面积为16,则该椭圆的短轴长为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题设条件推导出∠F1PF2=90°,
|PF1||PF2|=16,由椭圆定义知:|PF1|+|PF2|=2a,由此能求出椭圆的短轴长.
| 1 |
| 2 |
解答:
解:∵椭圆
+
=1(a>b>0)的两个焦点为F1、F2,
以F1F2为直径的圆与椭圆交于点P,
∴∠F1PF2=90°,
∵△F1PF2的面积为16,∴
|PF1||PF2|=16,
由椭圆定义知:|PF1|+|PF2|=2a,
又∵∠F1PF2=90°,
∴|PF1|2+|PF2|2+2|PF1||PF2|=4a2,
∴4c2+64=4a2,
∴4a2-4c2=4b2=64,
解得b=4.
∴椭圆的短轴长2b=8.
故答案为:8.
| x2 |
| a2 |
| y2 |
| b2 |
以F1F2为直径的圆与椭圆交于点P,
∴∠F1PF2=90°,
∵△F1PF2的面积为16,∴
| 1 |
| 2 |
由椭圆定义知:|PF1|+|PF2|=2a,
又∵∠F1PF2=90°,
∴|PF1|2+|PF2|2+2|PF1||PF2|=4a2,
∴4c2+64=4a2,
∴4a2-4c2=4b2=64,
解得b=4.
∴椭圆的短轴长2b=8.
故答案为:8.
点评:本题考查椭圆的短轴长的求法,是中档题,解题时要认真审题,注意椭圆简单性质的灵活运用.

练习册系列答案
相关题目
方程|x-1|=
表示的曲线是( )
| 1-(y-1) 2 |
| A、1个圆 | B、半圆 |
| C、2个半圆 | D、无法确定 |
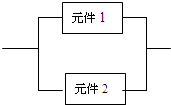 某个部件由两个电子元件按如图连接而成,当元件1或元件2正常工作,该部件正常工作.设两个电子元件的使用寿命(单位:小时)均服从正态分布N(800,100),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过800小时的概率为
某个部件由两个电子元件按如图连接而成,当元件1或元件2正常工作,该部件正常工作.设两个电子元件的使用寿命(单位:小时)均服从正态分布N(800,100),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过800小时的概率为