题目内容
已知p:a>
,q:直线x+y=0与圆x2+(y-a)2=1相离,则p是q的 .
| 2 |
考点:必要条件、充分条件与充要条件的判断,直线与圆的位置关系
专题:简易逻辑
分析:对于命题q:直线x+y=0与圆x2+(y-a)2=1相离,可得
>1,解得a>
或a<-
.即可判断出.
| |0+a| | ||
|
| 2 |
| 2 |
解答:
解:对于命题q:直线x+y=0与圆x2+(y-a)2=1相离,
∴
>1,即a>
或a<-
.
∴命题p是命题q的充分不必要条件.
故答案为:充分不必要条件.
∴
| |0+a| | ||
|
| 2 |
| 2 |
∴命题p是命题q的充分不必要条件.
故答案为:充分不必要条件.
点评:本题考查了直线与圆的位置关系、点到直线的距离公式、简易逻辑的判定,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
从半径R的球内接正方体的8个顶点及球心这9个点中任取2个点,则这两个点间的距离小于或等于半径的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
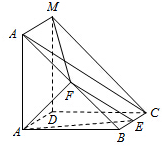 如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点.
如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点. 如图所示直三棱柱ABG-DCE中ABCD是边长为2的正方形,DE⊥平面ABCD,F为AG的中点,BE与平面ABCD所成角的正切值为
如图所示直三棱柱ABG-DCE中ABCD是边长为2的正方形,DE⊥平面ABCD,F为AG的中点,BE与平面ABCD所成角的正切值为