题目内容
11．若$\frac{5π}{2}$≤α≤$\frac{7π}{2}$，则$\sqrt{1+sinα}$+$\sqrt{1-sinα}$=$\sqrt{2-cosα}$．分析 利用平方法求解即可．
解答 解：由题意，令$\sqrt{1+sinα}$+$\sqrt{1-sinα}$=W，（W≥0）
可得1+sinα+1-sinα+$\sqrt{（1-sinα）（1+sinα）}$=W2，
有：2+|cosα|=W2，
∵$\frac{5π}{2}$≤α≤$\frac{7π}{2}$，
∴|cosα|=-cosα，
故得W=$\sqrt{2-cosα}$，
故答案为：$\sqrt{2-cosα}$．
点评 根据同角三角函数关系式和角象限的判断．属于基础题，
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
12．已知函数f（x）=x3-px2-qx的图象与x轴切于（1，0）点，则f（x）在[-1，1]的最大值、最小值分别为（ ）
| A． | 0，-4 | B． | $\frac{4}{27}$，-4 | C． | $\frac{4}{27}$，0 | D． | 2，0 |
16．
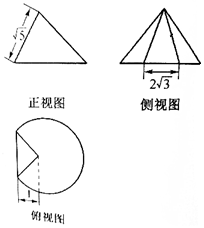一个圆锥被过顶点的平面截去了较少的一部分几何体，余下的几何体的三视图如图，则余下部分的几何体的体积为（ ）
一个圆锥被过顶点的平面截去了较少的一部分几何体，余下的几何体的三视图如图，则余下部分的几何体的体积为（ ）| A． | $\frac{8π}{3}$+$\sqrt{15}$ | B． | $\frac{16π}{3}$+$\sqrt{3}$ | C． | $\frac{8π}{3}$+$\frac{2\sqrt{3}}{3}$ | D． | $\frac{16π}{9}$+$\frac{2\sqrt{3}}{3}$ |
3．
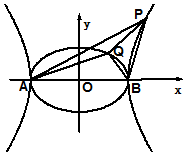已知A、B为椭圆$\frac{x^2}{4}+{y^2}$=1和双曲线$\frac{x^2}{4}-{y^2}$=1的公共顶点，P、Q分别为双曲线和椭圆上不同于两点A、B的动点，且有$\overrightarrow{PA}$+$\overrightarrow{PB}$=λ（$\overrightarrow{OA}$+$\overrightarrow{QB}$）（λ∈R，|λ|＞1），设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4，则k1+k2+k3+k4的值（ ）
已知A、B为椭圆$\frac{x^2}{4}+{y^2}$=1和双曲线$\frac{x^2}{4}-{y^2}$=1的公共顶点，P、Q分别为双曲线和椭圆上不同于两点A、B的动点，且有$\overrightarrow{PA}$+$\overrightarrow{PB}$=λ（$\overrightarrow{OA}$+$\overrightarrow{QB}$）（λ∈R，|λ|＞1），设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4，则k1+k2+k3+k4的值（ ）| A． | 大于0 | B． | 等于0 | ||
| C． | 小于0 | D． | 大于0，等于0，小于0都有可能 |
1．设数列{an}的通项公式为an=3n，且a2，a4，ak成等比数列，则数列k的值为（ ）
| A． | 9 | B． | 8 | C． | 7 | D． | 6 |