题目内容
17.已知动圆C经过点(1,0),且与直线x=-1相切,设圆心C的轨迹E.(1)求曲线E的方程;
(2)若直线l:y=kx+m(m≠0)与曲线E相交于A,B两个不同点,以AB为直径圆经过原点,证明:直线l必过一个定点.
分析 (1)由抛物线的定义可知轨迹为以(1,0)为焦点,以x=-1为准线的抛物线,
(2)联立方程组,利用根与系数的关系得出A,B的坐标,根据OA⊥OB列方程得出k与m的关系,从而确定直线l的定点.
解答 解:(1)∵圆C经过点(1,0),与直线x=-1相切,
∴圆心C到点(1,0)的距离等于到直线x=-1的距离,
∴圆心C的轨迹是以(1,0)为焦点,以x=-1为准线的抛物线,
∴曲线E的方程为y2=4x.
(2)联立方程组$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=kx+m}\end{array}\right.$,得k2x2+(2km-4)x+m2=0,
设A(x1,y1),B(x2,y2),则x1+x2=$\frac{4-2km}{{k}^{2}}$,x1x2=$\frac{{m}^{2}}{{k}^{2}}$,
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=2m2+$\frac{4m-2k{m}^{2}}{k}$,
∵以AB为直径圆经过原点,∴OA⊥OB,
∴$\frac{{y}_{1}}{{x}_{1}}•\frac{{y}_{2}}{{x}_{2}}$=-1,即x1x2+y1y2=0,
∴$\frac{{m}^{2}}{{k}^{2}}$+2m2+$\frac{4m-2k{m}^{2}}{k}$=0,∴m(m+4k)=0,
∵m≠0,∴m=-4k,
∴直线l的方程为y=kx-4k,即y=k(x-4),
直线l过定点(4,0).
点评 本题考查了抛物线的定义,直线与抛物线的位置关系,属于中档题.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
7.已知函数y=$\frac{1}{2}$x2的图象在点(x0,$\frac{1}{2}$x02)处的切线为l,若l也为函数y=lnx(0<x<1)的图象的切线,则x0必须满足( )
| A. | $\frac{\sqrt{2}}{2}$<x0<1 | B. | 1<x0<$\sqrt{2}$ | C. | $\sqrt{2}$<x0<$\sqrt{3}$ | D. | $\sqrt{3}$<x0<2 |
8.设{an}为各项均为正数的等比数列,且a2=$\frac{1}{3}$,a6=$\frac{1}{243}$.
(Ⅰ)求{an}的通项公式;
(Ⅱ)求和:T2n=a1-2a2+3a3-…-2na2n.
(Ⅰ)求{an}的通项公式;
(Ⅱ)求和:T2n=a1-2a2+3a3-…-2na2n.
9.若全集U=R,集合A={x|-1≤x<1},B={x|x≤0或x>2},则集合A∪∁UB=( )
| A. | {x|0<x<1} | B. | {x|-1≤x≤2} | C. | {x|-1<x<2} | D. | {x|0≤x≤1} |
20.设x,y满足约束条件$\left\{{\begin{array}{l}{2x-y-2≤0}\\{x-2y+2≥0}\\{x+y-2≥0}\end{array}}\right.$若z=mx+y取得最大值时的最优解有无穷多个,则实数m的值是( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 1 |
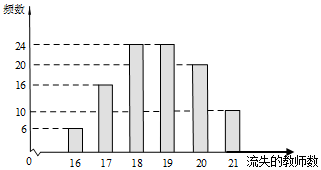 2017年两会继续关注了乡村教师的问题,随着城乡发展失衡,乡村教师待遇得不到保障,流失现象严重,教师短缺会严重影响乡村孩子的教育问题,为此,某市今年要为某所乡村中学招聘储备未来三年的教师,现在每招聘一名教师需要2万元,若三年后教师严重短缺时再招聘,由于各种因素,则每招聘一名教师需要5万元,已知现在该乡村中学无多余教师,为决策应招聘多少乡村教师搜集并整理了该市100所乡村中学在过去三年内的教师流失数,得到右面的柱状图:记x表示一所乡村中学在过去三年内流失的教师数,y表示一所乡村中学未来四年内在招聘教师上所需的费用(单位:万元),n表示今年为该乡村中学招聘的教师数,为保障乡村孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘
2017年两会继续关注了乡村教师的问题,随着城乡发展失衡,乡村教师待遇得不到保障,流失现象严重,教师短缺会严重影响乡村孩子的教育问题,为此,某市今年要为某所乡村中学招聘储备未来三年的教师,现在每招聘一名教师需要2万元,若三年后教师严重短缺时再招聘,由于各种因素,则每招聘一名教师需要5万元,已知现在该乡村中学无多余教师,为决策应招聘多少乡村教师搜集并整理了该市100所乡村中学在过去三年内的教师流失数,得到右面的柱状图:记x表示一所乡村中学在过去三年内流失的教师数,y表示一所乡村中学未来四年内在招聘教师上所需的费用(单位:万元),n表示今年为该乡村中学招聘的教师数,为保障乡村孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘