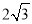题目内容
14.(1)求函数y=$\frac{2}{x}$+3x的值域.(2)已知x,y为正实数,且$\frac{x}{2}$+y=1,求$\frac{x+8y}{xy}$的最小值.
分析 (1)对x分类讨论,利用基本不等式的性质即可得出.
(2)利用“乘1法”与基本不等式的性质即可得出.
解答 解:(1)当x>0时,$y≥2\sqrt{\frac{2}{x}•3x}$=2$\sqrt{6}$,当且仅当x=$\frac{\sqrt{6}}{3}$时取等号.
当x<0时,同理可得y≤$-2\sqrt{6}$.
∴函数y=$\frac{2}{x}$+3x的值域为$(-∞,-2\sqrt{6}]$∪$[2\sqrt{6},+∞)$.
(2)∵x,y为正实数,且$\frac{x}{2}$+y=1,
∴$\frac{x+8y}{xy}$=$(\frac{x}{2}+y)$$(\frac{1}{y}+\frac{8}{x})$=5+$\frac{x}{2y}+\frac{8y}{x}$≥5+2$\sqrt{\frac{x}{2y}•\frac{8y}{x}}$=9,当且仅当x=4y=$\frac{4}{3}$时取等号.
∴$\frac{x+8y}{xy}$的最小值为9.
点评 本题考查了基本不等式的性质、简易逻辑的判定方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
6.已知复数z的共轭复数为$\overline{z}$,且满足z-2$\overline{z}$=2+3i,其中i为虚数单位,则|z|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 5 | D. | $\sqrt{5}$ |
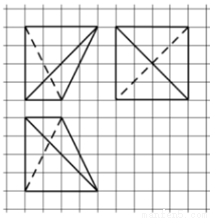
10.若椭圆上存在三点,使得这三点与椭圆中心恰好是一个正方形的四个顶点,则该椭圆的离心率为( )
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
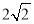 B.
B.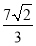 C.
C.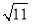 D.
D.