��Ŀ����
3����֪ԲO�ķ���Ϊx2+y2=100����1������A��10��20����ԲO�����ߣ������ߵķ��̣�
��2����ֱ��l��y=x+18��һ����ԲO�����ߣ������߳�����Сֵ��
��3����ֱ֪��y=kx+3��ԲO����M��N���㣬��|MN|��6$\sqrt{11}$����k��ȡֵ��Χ��
��4����ԲO����M��3��5������Һ�����ҷֱ�ΪAC��BD�����ı���ABCD�������
��5����AC��BDΪԲO���������ֱ���ң��Ҵ���ΪM��3��5�������ı���ABCD����������ֵ��
��6����ԲO������ֻ��4���㵽ֱ��l��x+y+��=0�ľ���Ϊ1����ʵ���˵�ȡֵ��Χ��
���� ��1�����A��10��20�������߷���Ϊkx-y-10k+20=0����$\frac{|20|}{\sqrt{{k}^{2}+1}}$=10����������߷��̣�
��2�������Բ��O��0��0����ֱ��l��y=x+18�ľ���d������Բ�뾶r=10����������߳�����Сֵ��
��3����Բ�ģ�0��0����ֱ��y=kx+3�ľ���d��$\sqrt{100-99}$=1��������������
��4��ԲO����M��3��5���������ֱ����������Ǵ�ֱ��ֱ�ߵ��ң��ɴ�������ı���ABCD�������
��5����d1��d2�ֱ���ԲO��AC��BD�ľ��룬��${{d}_{1}}^{2}+{{d}_{2}}^{2}$=9+25=34���ɻ�������ʽ���${d}_{1}={d}_{2}=\sqrt{17}$ʱ���ı���ABCD�����ȡ���ֵ��
��6���㵽ֱ�߾��빫ʽ�У�Բ��O��0��0����ֱ��l��x+y+��=0�ľ���d=$\frac{|��|}{\sqrt{2}}$���ɴ������ʵ���˵�ȡֵ��Χ��
��� �⣺��1��ԲO��x2+y2=100��Բ��O��0��0�����뾶r=10��
���A��10��20�������߷���Ϊy-20=k��x-10������kx-y-10k+20=0��
��$\frac{|20|}{\sqrt{{k}^{2}+1}}$=10�����k=$��\sqrt{3}$��
�����߷���Ϊy=$��\sqrt{3}$��x-10��+20��
��2����Բ��O��0��0����ֱ��l��y=x+18�ľ���d=$\frac{|18|}{\sqrt{2}}$=9$\sqrt{2}$��
Բ�뾶r=10��
�����߳�����СֵΪ��$\sqrt{{d}^{2}-{r}^{2}}$=$\sqrt{162-100}$=$\sqrt{62}$��
��3����ֱ��y=kx+3��ԲO����M��N���㣬|MN|��6$\sqrt{11}$��
��Բ�ģ�0��0����ֱ��y=kx+3�ľ���d=$\frac{|3|}{\sqrt{{k}^{2}+1}}$��$\sqrt{100-99}$=1��
���k$��2\sqrt{2}$��k��-2$\sqrt{2}$��
��4����ԲO��x2+y2=100��Բ��O��0��0�����뾶r=10��
ԲO����M��3��5������Һ�����ҷֱ�ΪAC��BD��
��AC=20��BD=2$\sqrt{100-��\sqrt{{3}^{2}+{5}^{2}}��^{2}}$=2$\sqrt{66}$��
���ı���ABCD�����S=$\frac{1}{2}��20��2\sqrt{66}$=20$\sqrt{66}$��
��5����d1��d2�ֱ���ԲO��AC��BD�ľ��룬��${{d}_{1}}^{2}+{{d}_{2}}^{2}$=9+25=34��
���ı���ABCD�����S=S��CAD+S��CAB=$\frac{1}{2}•AC•BD$
=$\frac{1}{2}•2\sqrt{100-{{d}_{1}}^{2}}•2\sqrt{100-{{d}_{2}}^{2}}$=2$\sqrt{��100-{{d}_{1}}^{2}����100-{{d}_{2}}^{2}��}$
=2$\sqrt{10{0}^{2}-100��{{d}_{1}}^{2}+{{d}_{2}}^{2}��+��{d}_{1}{d}_{2}��^{2}}$
=2$\sqrt{6600+��{d}_{1}{d}_{2}��^{2}}$��2$\sqrt{6600+��\frac{{{d}_{1}}^{2}+{{d}_{2}}^{2}}{2}��^{2}}$=2$\sqrt{6600+289}$=166��
��${d}_{1}={d}_{2}=\sqrt{17}$ʱ���ı���ABCD�����ȡ���ֵ166��
��6����ԲO������ֻ��4���㵽ֱ��l��x+y+��=0�ľ���Ϊ1��
�㵽ֱ�߾��빫ʽ�У�Բ��O��0��0����ֱ��l��x+y+��=0�ľ���Ϊ��
d=$\frac{|��|}{\sqrt{2}}$=1����æ�=$��\sqrt{2}$��
��-$\sqrt{2}���ˣ�\sqrt{2}$��
��ʵ���˵�ȡֵ��Χ�ǣ�-$\sqrt{2}$��$\sqrt{2}$����
���� ���⿼�����ߵķ��̡����߳�����Сֵ��ʵ��ȡֵ��Χ���ı�������������е��⣬����ʱҪ�������⣬ע��Բ�����ʡ��㵽ֱ�߾��빫ʽ����������ʽ�ĺ������ã�

 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�| A�� | y=log0.5|x| | B�� | y=${3}^{{x}^{2}}$ | C�� | y=-x2+x | D�� | y=cosx |
| A�� | -1-2i | B�� | -1+2i | C�� | 1+2i | D�� | 1-2i |
| ֱ��/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | �ϼ� |
| ���� | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
����Ϊ֤��һ̨�豸�����ܣ��Ӹ��豸�ӹ�������������ȡһ��������ֱ��ΪX�����������²���ʽ�������У�P��ʾ����¼���ʣ�����P����-�ң�X�ܦ�+�ң���0.6826����P����-2�ң�X�ܦ�+2�ң���0.9544����P����-3�ң�X�ܦ�+3�ң���0.9974�����й���Ϊ����ͬʱ����������������ʽ�����豸�ȼ�Ϊ�ף���������������������ȼ�Ϊ�ң�������������һ������ȼ�Ϊ������ȫ���������㣬��ȼ�Ϊ�������ж��豸M�����ܵȼ���
����ֱ��С�ڵ��ڦ�-2�һ�ֱ�������ڦ�+2�ҵ������Ϊ�Ǵ�Ʒ��������������Ʒ����ȡ2���������ǵ�ֱ��֮�����1mm�ĸ����Ƕ��٣�
| A�� | ���⡰��m��0����x2+x-m=0��ʵ�������������Ϊ����������x2+x-m=0��ʵ������m��0�� | |
| B�� | ��p��qΪ�����⣬��p��q��Ϊ������ | |
| C�� | ��x=1���ǡ�x2-3x+2=0���ij�ֲ���Ҫ���� | |
| D�� | ����Բ$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1��������ΪF1��F2������AB��F1�㣬���ABF2���ܳ�Ϊ20 |
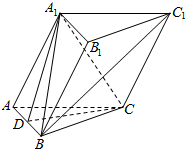 ��������ABC-A1B1C1�У�AA1��BC����A1AC=60�㣬AA1=AC=BC=$\sqrt{2}$��A1B=2��
��������ABC-A1B1C1�У�AA1��BC����A1AC=60�㣬AA1=AC=BC=$\sqrt{2}$��A1B=2�� ��ͼ������ƽ��ֱ������ϵxOy��x���ڵ�ƽ���ϣ�y�ᴹֱ�ڵ�ƽ�棬��λ����Ϊ1ǧ�ף�ij��λ������ԭ�㣮��֪�ڵ������Ĺ켣�ڷ���$y=kx-\frac{1}{20}��1+{k^2}��{x^2}��k��0��$��ʾ�������ϣ�����k�뷢�䷽���йأ��ڵ������ָ�ڵ���ص�ĺ����꣮
��ͼ������ƽ��ֱ������ϵxOy��x���ڵ�ƽ���ϣ�y�ᴹֱ�ڵ�ƽ�棬��λ����Ϊ1ǧ�ף�ij��λ������ԭ�㣮��֪�ڵ������Ĺ켣�ڷ���$y=kx-\frac{1}{20}��1+{k^2}��{x^2}��k��0��$��ʾ�������ϣ�����k�뷢�䷽���йأ��ڵ������ָ�ڵ���ص�ĺ����꣮