题目内容
2.已知函数y=2sin(ωx+φ)(ω>0),若存在x0∈R,使得f(x0+2)-f(x0)=4,则ω的最小值为$\frac{π}{2}$.分析 化简等式可得sin(ωx0+2ω+φ)-sin(ωx0+φ)=2,由正弦函数的性质可求ω=(k1-k2)π-$\frac{π}{2}$,k1、k2∈Z,结合ω>0求得ω的最小值.
解答 解:存在x0∈R,使得f(x0+2)-f(x0)=4,
即2sin[ω(x0+2)+φ]-2sin(ωx0+φ)=4成立,
∴sin(ωx0+2ω+φ)-sin(ωx0+φ)=2,
∴ωx0+2ω+φ=2k1π+$\frac{π}{2}$①,
ωx0+φ=2k2π+$\frac{3π}{2}$②,k1、k2∈Z;
由①②解得:ω=k1π-k2π-$\frac{π}{2}$,k1、k2∈Z;
又ω>0,∴ω的最小值是$\frac{π}{2}$.
故答案为:$\frac{π}{2}$.
点评 本题主要考查了正弦函数的图象和性质以及特殊角的三角函数值应用问题,属于中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
13.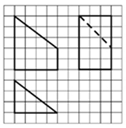 如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )
如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )
 如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )
如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )| A. | 12 | B. | 18 | C. | 20 | D. | 24 |
17.某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,在学习积极性高的25名学生中有7名不太主动参加班级工作,而在积极参加班级工作的24名学生中有6名学生学习积极性一般.
(1)填写下面列联表;
(2)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(3)试运用独立性检验的思想方法分析:能否在犯错误概率不超过0.001的前提下认为学生的学习积极性与对待班级工作的态度有关系.
(观测值表如下)
(1)填写下面列联表;
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | |||
| 学习积极性一般 | |||
| 合计 |
(3)试运用独立性检验的思想方法分析:能否在犯错误概率不超过0.001的前提下认为学生的学习积极性与对待班级工作的态度有关系.
(观测值表如下)
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
7.为了解某种产品的月广告费用x(单位:万元)对月销售量y(单位:万台)的影响,收集到如下5个月的统计数据:
根据上表中的数据可得线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=4.2,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$,据此估计,该产品的月广告费为13万元时的月销售量为( )
| 广告费x(万元) | 1 | 2 | 3 | 4 | 5 |
| 销售量y(万台) | 2 | 5 | 10 | 15 | 18 |
| A. | 30 | B. | 52 | C. | 57.2 | D. | 70 |
14.一个几何体的三视图如图所示,则它的体积为( )


| A. | $\frac{20}{3}$ | B. | $\frac{40}{3}$ | C. | $\frac{8}{3}$ | D. | 40 |
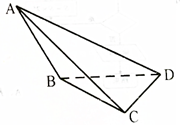 如图所示,在三棱锥A-BCD中,侧面ABD,ACD是全等的直角三角形,AD是公共的斜边且AD=$\sqrt{3}$,BD=CD=1,另一侧面ABC是正三角形.
如图所示,在三棱锥A-BCD中,侧面ABD,ACD是全等的直角三角形,AD是公共的斜边且AD=$\sqrt{3}$,BD=CD=1,另一侧面ABC是正三角形.