题目内容
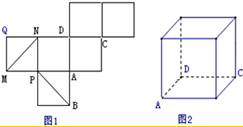图1是一个正方体的表面展开图，MN和PB是两条面对角线，请在图2的正方体中将MN和PB画出来，并就这个正方体解决下列问题（1）求证：MN∥平面PBD；
（2）求证：AQ⊥平面PBD；
（3）求二面角P-DB-M的余弦值．
考点：二面角的平面角及求法,直线与平面平行的判定,直线与平面垂直的判定
专题：空间位置关系与距离,空间角
分析：（1）画出MN和PB如图所示，求证：MN∥平面PBD，只需证MN∥BD；
（2）只需证BD⊥AQ，PD⊥AQ，通过直线与平面垂直的判定定理证明：AQ⊥平面PBD．
（3）建立空间直角坐标系如图所示，设正方体的棱长为1，求出相关点的坐标，利用平面的法向量求出二面角的余弦函数值．
（2）只需证BD⊥AQ，PD⊥AQ，通过直线与平面垂直的判定定理证明：AQ⊥平面PBD．
（3）建立空间直角坐标系如图所示，设正方体的棱长为1，求出相关点的坐标，利用平面的法向量求出二面角的余弦函数值．
解答：
（1）证明：在正方体ABCD-PMQN中
∵MN∥BD，
∴MN∥平面PBD
（2）证明：在正方体ABCD-PMQN中，
∵BD⊥AC，BD⊥CQ，AC∩CQ=C
∴BD⊥平面ACQ
∴BD⊥AQ，
同理可证：PD⊥AQ，
∵BD∩PD=D，
∴AQ⊥平面PBD
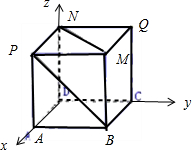
（3）解：建立空间直角坐标系如图所示，设正方体的棱长为1
则 A（1，0，0），Q（0，1，1），C（0，1，0）
由知平面PBD的一个法向量是
=（-1，1，1）
平面MBD的一个法向量是
=（-1，1，0）
∴cos＜
，
＞=
=
=
∴二面角P-DB-M的余弦值为
．
（1）证明：在正方体ABCD-PMQN中∵MN∥BD，
∴MN∥平面PBD
（2）证明：在正方体ABCD-PMQN中，
∵BD⊥AC，BD⊥CQ，AC∩CQ=C
∴BD⊥平面ACQ
∴BD⊥AQ，
同理可证：PD⊥AQ，
∵BD∩PD=D，
∴AQ⊥平面PBD
（3）解：建立空间直角坐标系如图所示，设正方体的棱长为1
则 A（1，0，0），Q（0，1，1），C（0，1，0）
由知平面PBD的一个法向量是
| AQ |
平面MBD的一个法向量是
| AC |
∴cos＜
| AQ |
| AC |
| ||||
|
|
| 2 | ||||
|
| ||
| 3 |
∴二面角P-DB-M的余弦值为
| ||
| 3 |
点评：综合法求二面角，往往需要作出平面角，这是几何中一大难点，而用向量法求解二面角无需作出二面角的平面角，只需求出平面的法向量，经过简单运算即可，从而体现了空间向量的巨大作用．二面角的向量求法：①若AB、CD分别是二面α-l-β的两个半平面内与棱l垂直的异面直线，则二面角的大小就是向量
与
的夹角； ②设
，
分别是二面角α-l-β的两个面α，β的法向量，则向量
，
的夹角（或其补角）的大小就是二面角的平面角的大小．
| AB |
| CD |
| n1 |
| n2 |
| n1 |
| n2 |
练习册系列答案
相关题目
已知定义在区间[-π，